
【题目】如图,在四边形ABCD中,∠B=90°,AD∥BC,BC=2AD,点E为边BC的中点.
(1)求证:四边形AECD为平行四边形;
(2)在CD边上取一点F,联结AF、 AC、 EF,设AC与EF交于点G,且∠EAF=∠CAD.
求证:△AEC∽△ADF;
(3)在(2)的条件下,当∠ECA=45°时.求: ![]() 的比值.
的比值.

【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)由E为BC中点,得到BC=2CE,再由BC=2AD,得到AD=CE,再由AD![]() CE,利用一组对边平行且相等的四边形为平行四边形即可得证;
CE,利用一组对边平行且相等的四边形为平行四边形即可得证;
(2)由四边形AECD为平行四边形,得到对角相等,再由已知角相等,利用两对角相等的三角形相似即可得证;
(3)AD=BE=CE=a,由∠ECA=![]() 得到△ABC为等腰直角三角形,即AB=BC=2a,
得到△ABC为等腰直角三角形,即AB=BC=2a,
Rt△ABE中,根据勾股定理表示出AE,由△AEC∽△ADF得比例,表示出DF.由CD-DF表示出CF,再由AE与DC平行得比例,即可求出所求式子之比.
试题解析:
(1)∵BC=2AD,点E为BC中点,
∴BC=2CE,
∴AD=CE,
∵AD![]() CE,
CE,
∴四边形AECD为平行四边形;
(2)∵四边形AECD为平行四边形,
∴∠D=∠AEC,
∵∠EAF=∠CAD,
∴∠EAC=∠DAF,
∴△AEC∽△ADF,
(3)设AD=BE=CE=a,由∠ECA=![]() 得到△ABC为等腰直角三角形,即AB=BC=2a,
得到△ABC为等腰直角三角形,即AB=BC=2a,
∴在Rt△ABE中,根据勾股定理得: ![]()
∵△AEC∽△ADF,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() .
.
∵AE∥DC,
∴![]() =
= .
.



科目:初中数学 来源: 题型:
【题目】为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如表数据:
轿车行驶的路程s(km) | 0 | 100 | 200 | 300 | 400 | … |
油箱剩余油量Q(L) | 50 | 42 | 34 | 26 | 18 | … |
(1)该轿车油箱的容量为______L,行驶150km时,油箱剩余油量为______L;
(2)根据上表的数据,写出油箱剩余油量Q(L)与轿车行驶的路程s(km)之间的表达式;
(3)某人将油箱加满后,驾驶该轿车从A地前往B地,到达B地时邮箱剩余油量为26L,求A,B两地之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张规格、质地相同的卡片,它们背面完全相同,正面图案分别是A 菱形,B 平行四边形,C 线段,D 角,将这四张卡片背面朝上洗匀后
(1)随机抽取一张卡片图案是轴对称图形的概率是 ;
(2)随机抽取两张卡片(不放回),求两张卡片卡片图案都是中心对称图形的概率,并用树状图或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数.(如下表)
每人加工零件数 | 54 | 45 | 30 | 24 | 21 | 12 |
人 数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理?为什么?如果不合理,请你设计一个较为合理的生产定额,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从百货大楼出发负责送货,向东走了 5 千米到达小明家,继续向东走了 1.5 千米到达小红家,然后向西走了 9.5 千米到达小刚家,最后返回百货大楼.
![]()
(1)以百货大楼为原点,向东为正方向,1 个单位长度表示 1 千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点 A 表示,小红家用点 B 表示,小刚家用点 C 表示)
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油 0.6 升,那么这辆货车此次送货共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了1元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2000元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3% 的损耗,第二次购进的水果有4% 的损耗,该水果店希望售完这些水果获利不低于3780元,则该水果每千克售价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
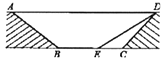
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面![]() 与通道
与通道![]() 平行),通道水平宽度
平行),通道水平宽度![]() 为8米,
为8米, ![]() ,通道斜面
,通道斜面![]() 的长为6米,通道斜面
的长为6米,通道斜面![]() 的坡度
的坡度![]() .
.
(1)求通道斜面![]() 的长为 米;
的长为 米;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面![]() 的坡度变缓,修改后的通道斜面
的坡度变缓,修改后的通道斜面![]() 的坡角为30°,求此时
的坡角为30°,求此时![]() 的长.(结果保留根号)
的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,DC⊥BC,AE 平分∠BAD,DE 平分∠ADC,以下结论:①∠AED=90°;②点 E 是 BC 的中点;③DE=BE;④AD=AB+CD;其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知点M(1,4),N(5,2),P(0,3),Q(3,0),过P,Q两点的直线的函数表达式为y=﹣x+3,动点P从现在的位置出发,沿y轴以每秒1个单位长度的速度向上移动,设移动时间为ts.
(1)若直线PQ随点P向上平移,则:
①当t=3时,求直线PQ的函数表达式.
②当点M,N位于直线PQ的异侧时,确定t的取值范围.
(2)当点P移动到某一位置时,△PMN的周长最小,试确定t的值.
(3)若点P向上移动,点Q不动.若过点P,Q的直线经过点A(x0,y0),则x0,y0需满足什么条件?请直接写出结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com