
分析 首先把原式的前三项提取$\frac{1+\sqrt{1-4a}}{2}$,计算括号里面的运算,结果为0,进一步得出结论即可.
解答 解:原式=$\frac{1+\sqrt{1-4a}}{2}$[($\frac{1+\sqrt{1-4a}}{2}$)2-$\frac{1+\sqrt{1-4a}}{2}$+a)+2014
=$\frac{1+\sqrt{1-4a}}{2}$[-a+$\frac{1+\sqrt{1-4a}}{2}$-$\frac{1+\sqrt{1-4a}}{2}$+a)+2014
=0+2014
=2014.
点评 此题考查二次根式的化简求值,利用提取公因式法分解因式,利用完全平方公式计算是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
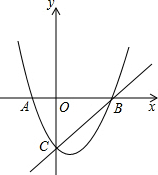 如图,抛物线 y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,M是直线BC下方的抛物线上一动点.
如图,抛物线 y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,M是直线BC下方的抛物线上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
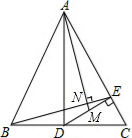 已知,如图所示,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC于点E,M是DE的中点,BE与AM交于点N.求证:∠EBC=∠DAM.
已知,如图所示,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC于点E,M是DE的中点,BE与AM交于点N.求证:∠EBC=∠DAM.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图:
如图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com