
分析 (1)寻找规律即可解决问题.
(2)利用等式的性质构造两个等式,S=1+2+22+23+…+29①,2S=2+22+23+24+…+210②,②-①即可解决问题.
(3)解法类似(2).
解答 解:(1)∵a1=3,a2=9=32,a3=27=33,a4=81=34,
∴每一项与前一项之比是3,a6=36,an=3n,
故答案分别为3,36,3n.
(2)∵S=1+2+22+23+…+29 ①,
2S=2+22+23+24+…+210 ②,
②-①得S=210-1,
故答案为210-1.
(3)设S=1+5+52+53+…+59 ①,
5S=5+52+53+54+…+510 ②
②-①得4S=510-5,
∴S=$\frac{{5}^{10}-5}{4}$.
故答案为$\frac{{5}^{10}-5}{4}$.
点评 本题考查规律题、学会利用等式的性质,构造两个等式,再利用解方程组的思想解决问题是解题的关键,属于中考常考题型.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
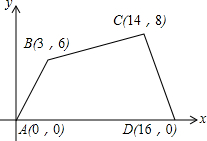 如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),
如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{x}$ | B. | $\sqrt{-x}$ | C. | -$\sqrt{x}$ | D. | ±$\root{3}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
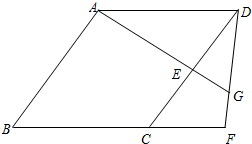 已知:如图,四边形ABCD是菱形,点E在边CD上,点F在BC的延长线上,CF=DE,AE的延长线与DF相交于点G.
已知:如图,四边形ABCD是菱形,点E在边CD上,点F在BC的延长线上,CF=DE,AE的延长线与DF相交于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com