
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点是点A(3,0),其部分图象如图,则下列结论:
①2a+b=0;
②b2﹣4ac<0;
③一元二次方程ax2+bx+c=0(a≠0)的另一个解是x=﹣1;
④点(x1,y1),(x2,y2)在抛物线上,若x1<0<x2,则y1<y2.
其中正确的结论是_____(把所有正确结论的序号都填在横线上)

科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,P是AD上一动点,连接BP,过点A作BP的垂线,垂足为F,交BD于点E,交CD于点G.
(1)当AB=AD,且P是AD的中点时,求证:AG=BP;
(2)在(1)的条件下,求![]() 的值;
的值;
(3)类比探究:若AB=3AD,AD=2AP,![]() 的值为 .(直接填答案)
的值为 .(直接填答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数![]() 的图象过点
的图象过点![]() .
.
![]() 求该函数的解析式;
求该函数的解析式;
![]() 过点
过点![]() 分别向
分别向![]() 轴和
轴和![]() 轴作垂线,垂足为
轴作垂线,垂足为![]() 和
和![]() ,求四边形
,求四边形![]() 的面积;
的面积;
![]() 求证:过此函数图象上任意一点分别向
求证:过此函数图象上任意一点分别向![]() 轴和
轴和![]() 轴作垂线,这两条垂线与两坐标轴所围成矩形的面积为定值.
轴作垂线,这两条垂线与两坐标轴所围成矩形的面积为定值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN.
(1)延长MP交CN于点E(如图②).
①求证:△BPM≌△CPE;
②求证:PM=PN;
(2)若直线a绕点A旋转到图③的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列的解答过程,然后再解答:
形如![]() 的化简,只要我们找到两个正数a、b,使a+b=m,ab=n,使得
的化简,只要我们找到两个正数a、b,使a+b=m,ab=n,使得![]() ,
,![]() ,那么便有:
,那么便有:![]() (a>b)
(a>b)
例如:化简![]()
解:首先把![]() 化为
化为![]() ,这里m=7,n=12,由于4+3=7,4×3=12
,这里m=7,n=12,由于4+3=7,4×3=12
即![]() ,
,![]()
∴![]() =
=![]()
(1)填空:![]() = ,
= ,![]() = ;
= ;
(2)化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一动点(不与点B,C重合),在AD右侧作△ADE,使得AD=AE,∠DAE=∠BAC,联结DE,CE。


(1)当点D在BC边上时,求证:EC=DB;
(2)当EC∥AB,若△ABD的最小角为20°,请写出ADB的度数,并对其中一个答案加以证明。
答:∠ADB的度数除了20°,还可能是 (直接写出所有答案,并对其中一个答案加以证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小马、小虎两人共同计算一道题:(x+a)(2x+b).由于小马抄错了a的符号,得到的结果是2x2﹣7x+3,小虎漏抄了第二个多项式中x的系数得到的结果是x2+2x﹣3.
(1)求a,b的值;
(2)细心的你请计算这道题的正确结果;
(3)当x=﹣1时,计算(2)中的代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
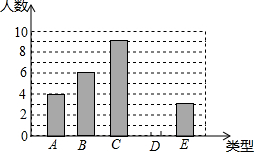
【题目】某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)补全条形统计图;
(2)求这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位750名职工共捐书多少本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com