练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，函数的图象过点．

    求该函数的解析式；

    过点分别向轴和轴作垂线，垂足为和，求四边形的面积；

    求证：过此函数图象上任意一点分别向轴和轴作垂线，这两条垂线与两坐标轴所围成矩形的面积为定值．

    【答案】 ；；矩形的面积为定值．

    【解析】

    （1）将点A的坐标代入反比例函数解析式，即可求出k值；

    （2）由于点A是反比例函数上一点，矩形ABOC的面积S=|k|．

    （3）设图象上任一点的坐标（x，y），根据矩形的面积公式，可得出结论．

    ∵函数的图象过点，

    ∴将点的坐标代入反比例函数解析式，

    得，解得：，

    ∴反比例函数的解析式为；

    ∵点是反比例函数上一点，

    ∴矩形的面积．

    设图象上任一点的坐标，

    ∴过这点分别向轴和轴作垂线，矩形面积为，

    ∴矩形的面积为定值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行，s（千米）表示汽车与甲地的距离，t（分）表示汽车行驶的时间，如图，L1，L2分别表示两辆汽车的s与t的关系．

    （1）L1表示哪辆汽车到甲地的距离与行驶时间的关系？

    （2）汽车B的速度是多少？

    （3）求L1，L2分别表示的两辆汽车的s与t的关系式．

    （4）2小时后，两车相距多少千米？

    （5）行驶多长时间后，A、B两车相遇？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“绿水青山就是金山银山”，为保护生态环境，A，B两村准备各自清理所属区域养鱼网箱和捕鱼网箱，每村参加清理人数及总开支如下表：

    村庄

    清理养鱼网箱人数/人

    清理捕鱼网箱人数/人

    总支出/元

    A

    15

    9

    57000

    B

    10

    16

    68000

    （1）若两村清理同类渔具的人均支出费用一样，求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元；

    （2）在人均支出费用不变的情况下，为节约开支，两村准备抽调40人共同清理养鱼网箱和捕鱼网箱，要使总支出不超过102000元，且清理养鱼网箱人数小于清理捕鱼网箱人数，则有哪几种分配清理人员方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：

    在学习《圆》这一章时，老师给同学们布置了一道尺规作图题：

    尺规作图：过圆外一点作圆的切线．

    已知：P为⊙O外一点．

    求作：经过点P的⊙O的切线．

    小敏的作法如下：如图，

    （1）连接OP，作线段OP的垂直平分线MN交OP于点C．

    （2）以点C为圆心，CO的长为半径作圆，交⊙O于A，B两点．

    （3）作直线PA，PB．

    老师认为小敏的作法正确．

    请回答：连接OA，OB后，可证∠OAP=∠OBP=90°，其依据是　 　；由此可证明直线PA，PB都是⊙O的切线，其依据是　 　．请写出证明过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】等边三角形ABC 中，BD是角平分线，点E在BC边的延长线上，且CD=CE，则∠BDE的度数是（ ）

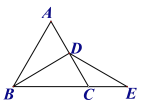
    A.90°B.100°C.120°D.无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，AB＝2，点M为正方形ABCD的边CD上的动点(与点C，D不重合)，连接BM，作MF⊥BM，与正方形ABCD的外角∠ADE的平分线交于点F.设CM＝x，△DFM的面积为y，则y与x之间的函数关系式为________________．

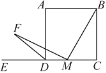
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】列方程解应用题：某商场经市场调查，预计一款夏季童装能获得市场青睐，便花费15000元购进了一批此款童装，上市后很快售罄．该店决定继续进货，由于第二批进货数量是第一批进货数量的2倍，因此单价便宜了10元，购进第二批童装一共花费了27000元．那该店所购进的第一批童装的价格是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点是点A（3，0），其部分图象如图，则下列结论：

    ①2a+b=0；

    ②b2﹣4ac＜0；

    ③一元二次方程ax2+bx+c=0（a≠0）的另一个解是x=﹣1；

    ④点（x1，y1），（x2，y2）在抛物线上，若x1＜0＜x2，则y1＜y2．

    其中正确的结论是_____（把所有正确结论的序号都填在横线上）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（本题6分）如图，已知△ABC，∠C=Rt∠，AC<BC，D为BC上一点，且到A，B两点的距离相等．

    （1）用直尺和圆规，作出点D的位置（不写作法，保留作图痕迹）；

    （2）连结AD，若∠B=37°，求∠CAD的度数．

    查看答案和解析>>

    同步练习册答案