
����Ŀ��С���μӰ��ѡ��������ݽ������������������������ʱһ��һƱ���������㡢���á�һ�㡱��ѡһͶƱ����ͼ��7λ��ί��С�����ݽ���硱������ͳ��ͼ��ȫ��50λͬѧ��������Ʊ��ͳ��ͼ��
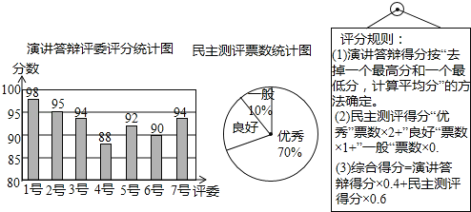
(1)����ί��С���ݽ����������������Լ���������Ϊ�����á�Ʊ��������Բ�ĽǶ�����
(2)��С�����ۺϵ÷��Ƕ��٣�
(3)�ھ�ѡ�У�С�������������÷�Ϊ82�֣���������ۺϵ÷ֲ�С��С�����ۺϵ÷֣������ݽ����÷�����Ҫ���ٷ֣�
���𰸡��⣺(1)��С���ݽ���������������94�֣�
��������Ϊ�����á�Ʊ�������ε�Բ�ĽǶ����ǣ�(1��10%��70%)��360�㣽72�㡣
(2)���ݽ����֣�(95��94��92��90��94)��5��93��
���������֣�50��70%��2��50��20%��1��80��
��С�����ۺϵ÷�Ϊ��93��0.4��80��0.6��85.2��
(3)����С�����ݽ����÷�Ϊx�֣��������⣬�ã�82��0.6��0.4x��85.2��
��ã�x��90��
��С�����ݽ����÷�����Ҫ90�֡�
��������(1)���������Ķ����������ͳ��ͼ���ɵó���ί��С���ݽ�����������������1��ȥһ���������ռ�İٷֱȣ��ٳ���360�㣬���ɵó���������Ϊ�����á�Ʊ��������Բ�ĽǵĶ���
(2)��ȥ��һ����߷ֺ�һ����ͷ֣�����ݽ����ֵ�ƽ���֣���������������֣��ٸ��ݹ涨���ɵó�С�����ۺϵ÷֡�
��3)����С�����ݽ����÷�Ϊx�֣����������г�����ʽ�����ɵó�С�����ݽ��������ٷ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
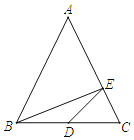
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��BC��6��EΪAC���ϵĵ���AE��2EC����D��BC����������BD��DE����BD��y��S��ABC��x����y��x�ĺ�����ϵʽΪ(����)
A.y��![]() x2+
x2+![]() B.y��
B.y��![]() x2+
x2+![]()
C.y��![]() x2+2D.y��
x2+2D.y��![]() x2+2
x2+2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y����![]() x+3��ͼ���뷴��������y��
x+3��ͼ���뷴��������y��![]() ��k��0����ͼ����A��B���㣬��A����x��Ĵ��ߣ�����ΪM����AOM���Ϊ2��
��k��0����ͼ����A��B���㣬��A����x��Ĵ��ߣ�����ΪM����AOM���Ϊ2��
��1�����������Ľ���ʽ��
��2����y������һ��P��ʹPA+PB��ֵ��С�����������Сֵ��P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ƽ���ı���ABCD���Խ���AC��BD�ཻ�ڵ�E����GΪAD���е㣬����CG��CG���ӳ��߽�BA���ӳ����ڵ�F������FD��
��1����֤��AB=AF��
��2����AG=AB����BCD=120�㣬�ж��ı���ACDF����״����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
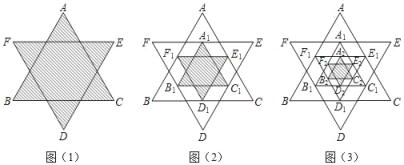
����Ŀ����ͼ��1������һ���������θ����ӳ�������һ������������AFBDCE���������Ϊ1��ȡ��ABC����DEF�����е㣬���ӳ�����������A1F1B1D1C1E1����ͼ��2������Ӱ���֣�ȡ��A1B1C1����D1E1F1�����е㣬���ӳ�����������A2F2B2D2C2E2����ͼ��3������Ӱ���֣������ȥ����������������A4F4B4D4C4E4�����Ϊ��������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
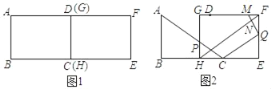
����Ŀ��������ȫ�ȵľ���ABCD��EFGH��ͼ1�ڷţ���D�͵�G�غϣ���C�͵�H�غϣ�����A��D��G����ͬһ��ֱ���ϣ�AB��6cm��BC��8cm����ͼ2����ABC��ͼ1λ�ó�������BC���������˶����ٶ�Ϊ1cm/s��AC��GH���ڵ�P��ͬʱ����Q�ӵ�E��������EF���������˶����ٶ�Ϊ1cm/s����Qֹͣ�˶�ʱ����ABCҲֹͣ�˶������˶�ʱ��Ϊt��s����0��t��6����
��1����tΪ��ֵʱ��CQ��FH��
��2������Q��QM��FH�ڵ�N����GF�ڵ�M���������GBCQM�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ��
��3���ڣ�2���������£��Ƿ����ijһʱ�̣�ʹ��M���߶�PC���д����ϣ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
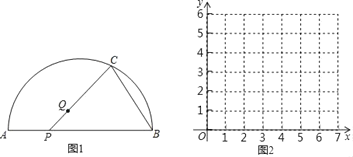
����Ŀ����ͼ����P��![]() ������AB��һ���㣬��Q��
������AB��һ���㣬��Q��![]() ����AB��Χ�ɵ�ͼ�ε��ڲ���һ���㣬������PQ��
����AB��Χ�ɵ�ͼ�ε��ڲ���һ���㣬������PQ��![]() �ڵ�C������BC����֪AB��6cm����A��P�����ľ���Ϊxcm��P��C�����ľ���Ϊy1cm��B��C�����ľ���Ϊy2cm��������P���A�غ�ʱ��x��ֵΪ0����
�ڵ�C������BC����֪AB��6cm����A��P�����ľ���Ϊxcm��P��C�����ľ���Ϊy1cm��B��C�����ľ���Ϊy2cm��������P���A�غ�ʱ��x��ֵΪ0����
Сƽ����ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
������Сƽ��̽�����̣��벹��������
��1�������±����Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���y��x�ļ����Ӧֵ��
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 5.37 | 4.06 | 2.83 | m | 3.86 | 4.83 | 5.82 |
y2/cm | 2.68 | 3.57 | 4.90 | 5.54 | 5.72 | 5.79 | 5.82 |
������m��ֵ�ǣ�����һλС������
��2����ͬһƽ��ֱ������ϵxOy�У������ȫ��ı��и�����ֵ����Ӧ�ĵ㣨x��y1������x��y2��������������y1��y2��ͼ��
��3����Ϻ���ͼ������⣺����BCPΪ����������ʱ��AP�ij���ԼΪ�� ��cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
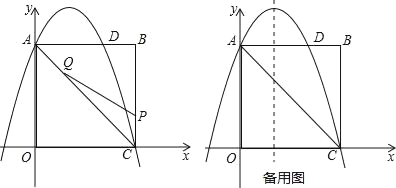
����Ŀ����ͼ���ھ���OABC�У���OΪԭ�㣬��A������Ϊ(0��8)����C������Ϊ(6��0)��������y����![]() x2+bx+c������A��C����AB���ڵ�D��
x2+bx+c������A��C����AB���ڵ�D��
(1)�������ߵĺ�������ʽ��
(2)��PΪ�߶�BC��һ������(�����C�غ�)����QΪ�߶�AC��һ�����㣬AQ��CP������PQ����CP��m����CPQ�����ΪS��
����S����m�ĺ�������ʽ��
����S���ʱ����������y����![]() x2+bx+c�ĶԳ���l�ϣ������ڵ�F��ʹ��DFQΪֱ�������Σ���ֱ��д�����з��������ĵ�F�����ꣻ�������ڣ���˵�����ɣ�
x2+bx+c�ĶԳ���l�ϣ������ڵ�F��ʹ��DFQΪֱ�������Σ���ֱ��д�����з��������ĵ�F�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() �뷴��������
�뷴��������![]() ��ͼ����A��1��4����B��4��n�����㣮
��ͼ����A��1��4����B��4��n�����㣮
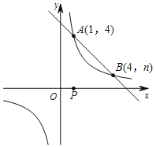
��1������������һ�κ����Ľ���ʽ��
��2��ֱ��д����x��0ʱ��![]() �Ľ⼯��
�Ľ⼯��
��3����P��x���ϵ�һ���㣬��ȷ����P������������꣬ʹPA+PB��С��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com