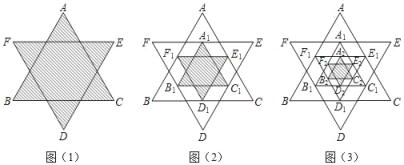
【题目】如图（1），将一个正六边形各边延长，构成一个正六角星形AFBDCE，它的面积为1；取△ABC和△DEF各边中点，连接成正六角星形A1F1B1D1C1E1，如图（2）中阴影部分；取△A1B1C1和△D1E1F1各边中点，连接成正六角星形A2F2B2D2C2E2，如图（3）中阴影部分；如此下去…，则正六角星形A4F4B4D4C4E4的面积为（ ）
A. 
B. 
C. 
D. 
阅读快车系列答案科目：初中数学 来源： 题型：
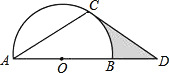
【题目】如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC=CD，∠ACD=120°.
（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为2，求图中阴影部分的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法中正确的有_____．（填序号）
①
的平方根是±3
②绝对值等于它本身的数一定是正数
③关于x的一元二次方程（m﹣2）x2+2x+1＝0有实数根，则m的取值范围是m≤3
④如果一个多边形的内角和是外角和的3倍，则这个多边形的边数是8
⑤观察下列单项式2x，﹣4x2，8x3，﹣16x4，…，则第7个单项式是128x7
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y＝a（x﹣1）2+k的图象与x轴交于A，B两点，AB＝4，与y轴交于C点，E为抛物线的顶点，∠ECO＝135°．
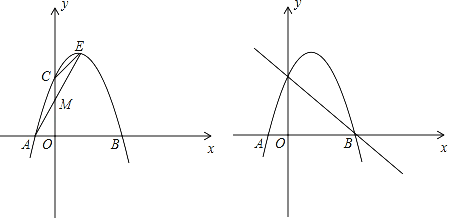
（1）求二次函数的解析式；
（2）若P在第四象限的抛物线上，连接AE交y轴于点M，连接PE交x轴于点N，连接MN，且S△EAP＝3S△EMN，求点P的坐标；
（3）过直线BC上两点P，Q（P在Q的左边）作y轴的平行线，分别交抛物线于N，M，若四边形PQMN为菱形，求直线MN的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某企业生产并销售某种产品，假设销售量与产量相等，如图中的折线ABD表示该产品每千克生产成本y1（单位：元）与产量x（单位：kg）之间的函数关系；线段CD表示每千克的销售价y2（单位：元）与产量x（单位：kg）之间的函数关系．
（1）请解释图中点D的横坐标、纵坐标的实际意义．
（2）求线段AB所表示的y1与x之间的函数表达式．
（3）当0≤x≤90时，销售该产品获得的利润与产量的关系式是 ；当90≤x≤130时，销售该产品获得的利润与产量的关系式是 ；总之，当产量为 kg时，获得的利润最大，最大利润是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明参加班长竞选，需进行演讲答辩与民主测评，民主测评时一人一票，按“优秀、良好、一般”三选一投票．如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图．
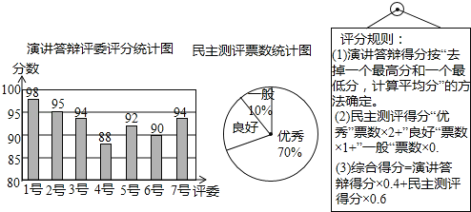
(1)求评委给小明演讲答辩分数的众数，以及民主测评为“良好”票数的扇形圆心角度数；
(2)求小明的综合得分是多少？
(3)在竞选中，小亮的民主测评得分为82分，如果他的综合得分不小于小明的综合得分，他的演讲答辩得分至少要多少分？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，Rt△ABC中，∠ACB＝90°，AC＝5，BC＝12，点D在边AB上，以AD为直径的⊙O，与边BC有公共点E，则AD的最小值是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠C=90°，AC=BC=3cm.动点P从点A出发，以
cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发，以1cm/s的速度沿折线AC
CB方向运动到点B.设△APQ的面积为y（cm2）.运动时间为x（s），则下列图象能反映y与x之间关系的是 （ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明在学了尺规作图后，通过“三弧法”作了一个△ACD，其作法步骤是：①作线段AB，分别以A，B为圆心，AB长为半径画弧，两弧的交点为C；②以B为圆心，AB长为半径画弧交AB的延长线于点D；③连结AC，BC，CD．下列说法不正确的是（ ）
A.∠A＝60°B.△ACD是直角三角形
C.BC＝
CDD.点B是△ACD的外心
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
