
【题目】如图,一次函数y=﹣![]() x+3的图象与反比例函数y=
x+3的图象与反比例函数y=![]() (k>0)的图象交于A,B两点,过A点作x轴的垂线,垂足为M,△AOM面积为2.
(k>0)的图象交于A,B两点,过A点作x轴的垂线,垂足为M,△AOM面积为2.
(1)求反比例函数的解析式;
(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.

【答案】(1)y=![]() ;(2)y=﹣
;(2)y=﹣![]() x+
x+![]() ,点P的坐标为(0,
,点P的坐标为(0,![]() ).
).
【解析】
(1)利用反比例函数k的几何意义即可求出反比例函数的解析式;
(2)先把解析式联立组成方程组求出A、B两点的坐标,再利用轴对称的性质找到符合条件的点P的位置,利用一次函数与y轴的交点求出P点坐标,再利用勾股定理求出最小距离和.
(1)设A点的坐标为(a,b),则OM=a,AM=b,
∵△AOM面积为2,
∴![]() ab=2,
ab=2,
∴ab=4,
∵点A在反比例函数图象上,
∴k=4,
∴反比例函数的解析式为y=![]() ;
;
(2)依题意可知,A、B两点的坐标为方程组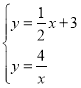 的解,
的解,
解方程组得:点A的坐标为(2,2),点B的坐标为(4,1),
点A关于y轴的对称点A′的坐标为(﹣2,2),连接A′B,交y轴于点P,点P即为所求,此时PA+PB最小,最小值为A′B的长.
由勾股定理得:A′B=![]() .
.
设直线A′B的解析式为y=kx+b,带入A′,B的坐标得![]() ,
,
解得: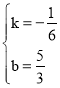 ,
,
∴![]() ,点P的坐标为(0,
,点P的坐标为(0,![]() ).
).


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】已知如图,四边形ABCD为矩形,点O是AC的中点,过点O的一直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO,若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB:OE=3:2,其中正确结论是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
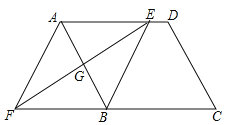
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
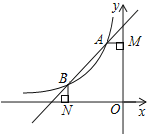
【题目】如图所示,函数y1=kx+b的图象与函数![]() (x<0)的图象交于A(a﹣2,3)、B(﹣3,a)两点.
(x<0)的图象交于A(a﹣2,3)、B(﹣3,a)两点.
(1)求函数y1、y2的表达式;
(2)过A作AM⊥y轴,过B作BN⊥x轴,试问在线段AB上是否存在点P,使S△PAM=3S△PBN?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的有_____.(填序号)
①![]() 的平方根是±3
的平方根是±3
②绝对值等于它本身的数一定是正数
③关于x的一元二次方程(m﹣2)x2+2x+1=0有实数根,则m的取值范围是m≤3
④如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是8
⑤观察下列单项式2x,﹣4x2,8x3,﹣16x4,…,则第7个单项式是128x7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x﹣1)2+k的图象与x轴交于A,B两点,AB=4,与y轴交于C点,E为抛物线的顶点,∠ECO=135°.
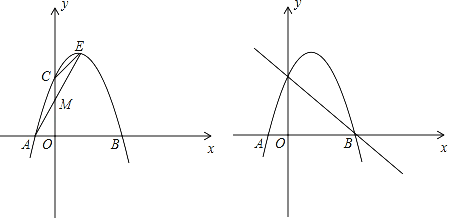
(1)求二次函数的解析式;
(2)若P在第四象限的抛物线上,连接AE交y轴于点M,连接PE交x轴于点N,连接MN,且S△EAP=3S△EMN,求点P的坐标;
(3)过直线BC上两点P,Q(P在Q的左边)作y轴的平行线,分别交抛物线于N,M,若四边形PQMN为菱形,求直线MN的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加班长竞选,需进行演讲答辩与民主测评,民主测评时一人一票,按“优秀、良好、一般”三选一投票.如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图.
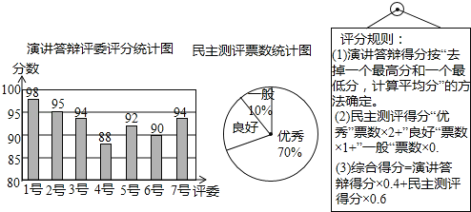
(1)求评委给小明演讲答辩分数的众数,以及民主测评为“良好”票数的扇形圆心角度数;
(2)求小明的综合得分是多少?
(3)在竞选中,小亮的民主测评得分为82分,如果他的综合得分不小于小明的综合得分,他的演讲答辩得分至少要多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+bx+c的顶点为C,对称轴为直线x=1,且经过点A(3,-1),与y轴交于点B.
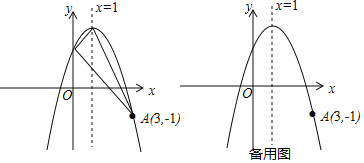
(1)求抛物线的解析式;
(2)判断△ABC的形状,并说明理由;
(3)经过点A的直线交抛物线于点P,交x轴于点Q,若S△OPA=2S△OQA,试求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com