
【题目】如图,在△ABC中,高AD和BE交于点H,且∠1=∠2=22.5°,下列结论正确的有( )
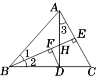
①∠1=∠3;②BD+DH=AB;③2AH=BH;④若CD=![]() ,则BH=3;⑤若DF⊥BE于点F,则AE-DF=FH.
,则BH=3;⑤若DF⊥BE于点F,则AE-DF=FH.
A.①②④B.①②⑤C.②③④D.③④⑤
【答案】B
【解析】
①由直角三角形的性质得出∠1=∠3,①正确;
②证出△ABD是等腰直角三角形,得出AD=BD,证明△BDH≌△ADC(ASA),得出DH=CD,BH=AC,得出BD+DH=AB,②正确;
③由BH=AC,当AC=2AH时,2AH=BH,③错误;
④连接CH,由全等三角形的性质得出DH=DC=![]() ,得出△CDH是等腰直角三角形,得出CH=
,得出△CDH是等腰直角三角形,得出CH=![]() CD=2,∠CHD=45°,证出AH=CH=2,得出BD=AD=2+
CD=2,∠CHD=45°,证出AH=CH=2,得出BD=AD=2+![]() ,由勾股定理即可得出④错误;
,由勾股定理即可得出④错误;
⑤作DK⊥AC于K,则DF=EK,证明△DFH≌△DKC(AAS),得出FH=KC,DF=DK,证出AB=CB,由等腰三角形的性质得出AE=CE,即可得出AEFH=DF,⑤正确;即可得出结论.
解:①∵∠1=∠2=22.5°,
又∵AD是高,
∴AD⊥BC,
∴∠2+∠C=∠3+∠C,
∴∠1=∠3,①正确;
②∵∠1=∠2=22.5°,
∴∠ABD=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵AD⊥BC,
∴∠BDH=∠ADC=90°,
在△BDH和△ADC中,
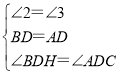
∴△BDH≌△ADC(ASA),
∴DH=CD,BH=AC,
∵AB=BC,
∴BD+DH=AB,②正确;
③∵BH=AC,当AC=2AH时,2AH=BH,③错误;
④连接CH,如图1所示:
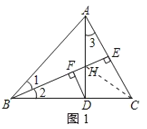
∵△BDH≌△ADC,
∴DH=DC=![]() ,
,
∴△CDH是等腰直角三角形,
∴CH=![]() CD=2,∠CHD=45°,
CD=2,∠CHD=45°,
∵∠3=∠2=22.5°,
∴∠HCA=22.5°=∠3,
∴AH=CH=2,
∴BD=AD=2+![]() ,
,
∴BH2=BD2+DH2=(2+![]() )2+(
)2+(![]() )2≠9,
)2≠9,
∴BH≠3,④错误;
⑤作DK⊥AC于K,如图2所示:
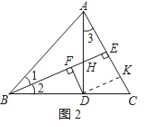
则DF=EK,∠DKC=90°,∠C+∠CDK=∠C+∠3,
∴∠CDK=∠3,
∵BE⊥AC,DF⊥BE,
∴DF∥AC,∠DFH=90°=∠DKC,
∴∠FDH=∠CDK,
在△DFH和△DKC中,
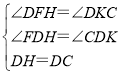 ,
,
∴△DFH≌△DKC(AAS),
∴FH=KC,DF=DK,
∵∠1=∠2,BE⊥AC,
∴∠BAC=∠BCA,
∴AB=CB,
∴AE=CE,
∵CE=KC+EK,DF=EK,
∴AE=FH+DF,
∴AEFH=DF,⑤正确.
故选:B.


科目:初中数学 来源: 题型:
【题目】定义一种新运算“”:观察下列各式:
23=2×3+3=9;3(﹣1)=3×3﹣1=8;
44=4×3+4=16:5(﹣3)=5×3﹣3=12
(1)请你想一想:ab= ;
(2)已知(a+3)2与|b﹣1|互为相反数,c与a互为倒数,试求c(ab)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?
查看答案和解析>>
科目:初中数学 来源: 题型:
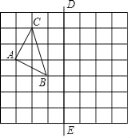
【题目】如图,在所给的网格图中,完成下列各题(用直尺画图,否则不给分)
(1)画出格点△ABC关于直线DE的对称的△A1B1C1;
(2)在DE上画出点P,使PA+PC最小;
(3)在DE上画出点Q,使QA﹣QB最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
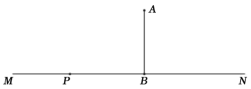
【题目】为了积极响应国家新农村建设,遂宁市某镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路MN的一侧点A处有一村庄,村庄A到公路MN的距离为600米,假使宣讲车P周围1000米以内能听到广播宣传,宣讲车P在公路MN上沿PN方向行驶时:
(1)请问村庄能否听到宣传,请说明理由;
(2)如果能听到,已知宣讲车的速度是200米/分钟,那么村庄总共能听到多长时间的宣传?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在宁波慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图。

(1)这50名同学捐款的众数为___元,中位数为___元;
(2)该校共有600名学生参与捐款,请估计该校学生的捐款总数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商人制成了一个如图所示的转盘,取名为“开心大转盘”,游戏规定:参与者自由转动转盘,转盘停止后,若指针指向字母“A”,则收费2元,若指针指向字母“B”,则奖励3元;若指针指向字母“C”,则奖励1元.一天,前来寻开心的人转动转盘80次,你认为该商人是盈利的可能性大还是亏损的可能性大?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区2015年投入教育经费2900万元,2017年投入教育经费3509万元.
(1)求2015年至2017年该地区投入教育经费的年平均增长率;
(2)按照义务教育法规定,教育经费的投入不低于国民生产总值的百分之四,结合该地区国民生产总值的情况,该地区到2019年需投入教育经费4250万元.如果按(1)中教育经费投入的增长率,到2019年该地区投入的教育经费是否能达到4250万元?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com