练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

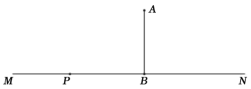
    【题目】为了积极响应国家新农村建设，遂宁市某镇政府采用了移动宣讲的形式进行宣传动员．如图，笔直公路MN的一侧点A处有一村庄，村庄A到公路MN的距离为600米，假使宣讲车P周围1000米以内能听到广播宣传，宣讲车P在公路MN上沿PN方向行驶时：

    （1）请问村庄能否听到宣传，请说明理由；

    （2）如果能听到，已知宣讲车的速度是200米/分钟，那么村庄总共能听到多长时间的宣传？

    【答案】（1）村庄能听到宣传，见解析（2）村庄总共能听到8分钟的宣传

    【解析】

    （1）根据村庄A到公路MN的距离为600米＜1000米，于是得到结论；

    （2）根据勾股定理得到BP＝BQ＝800米，求得PQ＝1600米，于是得到结论．

    解：（1）村庄能听到宣传，

    理由：∵村庄A到公路MN的距离为600米＜1000米

    ∴村庄能听到宣传

    （2）如图：假设当宣讲车行驶到P点开始影响村庄，行驶QD点结束对村庄的影响

    则AP＝AQ＝1000米，AB＝600米

    ∴BP＝BQ＝米

    ∴PQ＝1600米

    ∴影响村庄的时间为：1600÷200＝8分钟

    ∴村庄总共能听到8分钟的宣传．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一副直角三角尺叠放如图1所示，现将45°的三角尺ADE固定不动，将含30的三角尺ABC绕顶点A顺时针转动，使两块三角尺至少有一组边互相平行，如图2，当∠BAD=15°时，BC∥DE，则∠BAD(0°＜∠BAD＜180°)其它所有可能符合条件的度数为（ ）

    A.60°和135°B.45°、60°、105°、135°C.30°和45°D.以上都有可能

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】温州市处于东南沿海，夏季经常遭受台风袭击．一次，温州气象局测得台风中心在温州市A的正西方向300千米的B处（如图），以每小时10千米的速度向东偏南30°的BC方向移动，并检测到台风中心在移动过程中，温州市A将受到影响，且距台风中心200千米的范围是受台风严重影响的区域．则影响温州市A的时间会持续多长？（　　）

    A. 5 B. 6 C. 8 D. 10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】俗话说“一铺养三代”。曾经，在市区繁华地段租一间门面，做点小生意，是不少人的生存之道。如今，这样的传统致富门道正在不断受到挑战。某服装店主，顺应时代潮流，在实体店销售的同时，开始网上销售。

    （1）该店主某月线上线下共销售某款童装200件，其中网上销售量不低于实体销售量的4倍，求该店主该月实体销售量最多为多少？

    （2）已知该店主5月实体销售该童装100件，每件获利18元；网上销售200件，每件获利12元。6月店主加大网上销售力度，网上销售每件获利较5月减少m%,但销售量比5月增加了2m%,实体店每件获利不变，销售量比5月减少了m%。结果该店主5月、6月线上线下获利总金额相同，求m的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，高AD和BE交于点H，且∠1＝∠2＝22.5°，下列结论正确的有（　　）

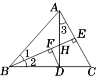
    ①∠1＝∠3；②BD+DH＝AB；③2AH＝BH；④若CD＝，则BH＝3；⑤若DF⊥BE于点F，则AE－DF＝FH．

    A.①②④B.①②⑤C.②③④D.③④⑤

    查看答案和解析>>

    科目：初中数学 来源： 题型：

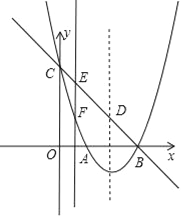
    【题目】如图，抛物线y=ax2+bx+c（a≠0）的顶点坐标为（2，﹣1），图象与y轴交于点C（0，3），与x轴交于A、B两点．

    （1）求抛物线的解析式；

    （2）设抛物线对称轴与直线BC交于点D，连接AC、AD，求△ACD的面积；

    （3）点E为直线BC上的任意一点，过点E作x轴的垂线与抛物线交于点F，问是否存在点E使△DEF为直角三角形？若存在，求出点E坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O的半径为1，经过点A（2，0）的直线与⊙O相切于点B，与y轴相交于点C．

    （1）求AB的长；

    （2）如果把直线AC看成一次函数y=kx+b的图象，试求k、b．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，O为坐标原点．△ABC的边BC在x轴上，A、C两点的坐标分别为A（0，m）、C（n，0），B（﹣5，0），且，点P从B出发，以每秒2个单位的速度沿射线BO匀速运动，设点P运动时间为t秒．

    （1）求A、C两点的坐标；

    （2）连接PA，用含t的代数式表示△POA的面积；

    （3）当P在线段BO上运动时，是否存在一点P,使△PAC是等腰三角形？若存在，请写出满足条件的所有P点的坐标并求t的值；若不存在，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：y=﹣10x+500，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的60%．

    （1）设小明每月获得利润为w（元），求每月获得利润w（元）与销售单价x（元）之间的函数关系式，并确定自变量x的取值范围．

    （2）当销售单价定为多少元时，每月可获得最大利润？每月的最大利润是多少？

    （3）如果小明想要每月获得的利润不低于2000元，那么小明每月的成本最少需要多少元？（成本=进价×销售量）

    查看答案和解析>>

    同步练习册答案