
【题目】若直线L1经过点(0,2),L2经过点(2,1),且L1与L2关于x轴对称,则L1与L2的交点坐标为_____.
【答案】(2.0)
【解析】
根据对称的性质得出两个点关于x轴对称的对称点,再根据待定系数法确定函数关系式,求出一次函数与x轴的交点即可.
∵直线l1经过点(0,2),l2经过点(2,1),且l1与l2关于x轴对称,
∴两直线相交于x轴上,
∵直线l1经过点(0,2),l2经过点(2,1),且l1与l2关于x轴对称,
∴直线l1经过点(2,﹣1),l2经过点(0,﹣2),
把(0,2)和(2,﹣1)代入直线l1的解析式y=kx+b,
则![]() ,
,
解得: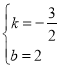 ,
,
故直线l1的解析式为:y=﹣![]() x+3,
x+3,
可得l1与l2的交点坐标为l1与l2与x轴的交点,解得:x=2,
即l1与l2的交点坐标为(2,0).
故答案为(2,0).


科目:初中数学 来源: 题型:
【题目】已知a=2 002x+2 003,b=2 002x+2 004,c=2 002x+2 005,则多项式a2+b2+c2-ab-bc-ca的值为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图①,在△ABC 中,D、E 分别是 AB、AC 上的点,AB=AC,AD=AE,然后将△ADE 绕点 A 顺时针旋转一定角度,连接 BD,CE,得到图②,将 BD、CE 分别延长至 M、N,使 DM=![]() BD,EN=
BD,EN=![]() CE,得到图③,请解答下列问题:
CE,得到图③,请解答下列问题:
(1)在图②中,BD 与 CE 的数量关系是 ;
(2)在图③中,猜想 AM 与 AN 的数量关系,∠MAN 与∠BAC 的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的例题:
解方程![]()
解:(1)当x≥0时,
原方程化为x2 – x –2=0,
解得:x1=2,x2= - 1(不合题意,舍去)
(2)当x<0时,
原方程化为x2 + x –2=0,
解得:x1=1,(不合题意,舍去)x2= -2
∴原方程的根是x1=2, x2= - 2
(3)请参照例题解方程![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人设摊“摸彩”,只见他手持一袋,内装大小、质量完全相同的![]() 个红球、
个红球、![]() 个白球,每次让顾客“免费”从袋中摸出两球,如果两球的颜色相同,顾客得
个白球,每次让顾客“免费”从袋中摸出两球,如果两球的颜色相同,顾客得![]() 元钱,否则顾客付给这人
元钱,否则顾客付给这人![]() 元钱,请你判断一下该活动对顾客________(填“合算”或“不合算”).
元钱,请你判断一下该活动对顾客________(填“合算”或“不合算”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州市处于东南沿海,夏季经常遭受台风袭击.一次,温州气象局测得台风中心在温州市A的正西方向300千米的B处(如图),以每小时10![]() 千米的速度向东偏南30°的BC方向移动,并检测到台风中心在移动过程中,温州市A将受到影响,且距台风中心200千米的范围是受台风严重影响的区域.则影响温州市A的时间会持续多长?( )
千米的速度向东偏南30°的BC方向移动,并检测到台风中心在移动过程中,温州市A将受到影响,且距台风中心200千米的范围是受台风严重影响的区域.则影响温州市A的时间会持续多长?( )

A. 5 B. 6 C. 8 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知a为正整数,关于x的不等式组![]() 的整数解仅2、3、4,则a的最大值是_____.
的整数解仅2、3、4,则a的最大值是_____.
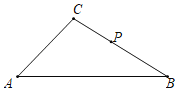
(2)如图,△ABC中,AC=![]() ,∠A=45°,∠B=30°,P是BC边上一点(不含端点),将PC绕着点P逆时针旋转得到PC′,旋转角α(0<α<180°),若旋转过程中,点C′始终落在△ABC内部(不包含边上),则PC的取值范围是_____.
,∠A=45°,∠B=30°,P是BC边上一点(不含端点),将PC绕着点P逆时针旋转得到PC′,旋转角α(0<α<180°),若旋转过程中,点C′始终落在△ABC内部(不包含边上),则PC的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,高AD和BE交于点H,且∠1=∠2=22.5°,下列结论正确的有( )
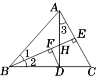
①∠1=∠3;②BD+DH=AB;③2AH=BH;④若CD=![]() ,则BH=3;⑤若DF⊥BE于点F,则AE-DF=FH.
,则BH=3;⑤若DF⊥BE于点F,则AE-DF=FH.
A.①②④B.①②⑤C.②③④D.③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com