
【题目】(1)已知a为正整数,关于x的不等式组![]() 的整数解仅2、3、4,则a的最大值是_____.
的整数解仅2、3、4,则a的最大值是_____.
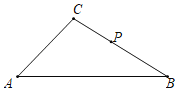
(2)如图,△ABC中,AC=![]() ,∠A=45°,∠B=30°,P是BC边上一点(不含端点),将PC绕着点P逆时针旋转得到PC′,旋转角α(0<α<180°),若旋转过程中,点C′始终落在△ABC内部(不包含边上),则PC的取值范围是_____.
,∠A=45°,∠B=30°,P是BC边上一点(不含端点),将PC绕着点P逆时针旋转得到PC′,旋转角α(0<α<180°),若旋转过程中,点C′始终落在△ABC内部(不包含边上),则PC的取值范围是_____.
【答案】﹣20 0<PC<4
【解析】
(1)首先解不等式组,用a表示出不等式组的解集,根据不等式的整数解仅有2,3,4,即可确定a的值,从而求解;
(2)过C作CD⊥AB于D,过P作PH⊥AB于H,设CP=x=PC',则BP=12﹣x,PH=![]() (12﹣x),依据旋转过程中,点C′始终落在△ABC内部(不包括边上),即可得到PC'<PH,即x<
(12﹣x),依据旋转过程中,点C′始终落在△ABC内部(不包括边上),即可得到PC'<PH,即x<![]() (12﹣x),进而得出PC的取值范围.
(12﹣x),进而得出PC的取值范围.
(1)解不等式组![]() 得:﹣
得:﹣![]() <x≤
<x≤![]() ,
,
∵整数解仅有2,3,4,
∴1≤﹣![]() <2,解得:﹣40<a≤﹣20,
<2,解得:﹣40<a≤﹣20,
∴a的最大值为﹣20,
故答案为:﹣20;
(2)如图,过C作CD⊥AB于D,过P作PH⊥AB于H,
∵AC=6![]() ,∠A=45°,∠B=30°,
,∠A=45°,∠B=30°,
∴AD=CD=6,BC=2CD=12,
设CP=x=PC',则BP=12﹣x,PH=![]() (12﹣x),
(12﹣x),
∵旋转过程中,点C′始终落在△ABC内部(不包括边上),
∴PC'<PH,即x<![]() (12﹣x),
(12﹣x),
解得x<4,
又∵PC>0,
∴0<PC<4,
故答案为:0<PC<4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?
查看答案和解析>>
科目:初中数学 来源: 题型:
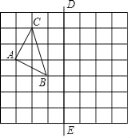
【题目】如图,在所给的网格图中,完成下列各题(用直尺画图,否则不给分)
(1)画出格点△ABC关于直线DE的对称的△A1B1C1;
(2)在DE上画出点P,使PA+PC最小;
(3)在DE上画出点Q,使QA﹣QB最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在宁波慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图。

(1)这50名同学捐款的众数为___元,中位数为___元;
(2)该校共有600名学生参与捐款,请估计该校学生的捐款总数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在BA的延长线上,CA=AO,点D在⊙O上,∠ABD=30°.
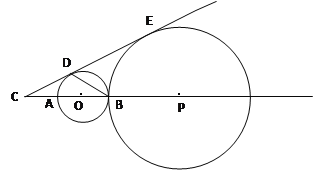
⑴求证:CD是⊙O的切线;
⑵若点P在直线AB上,⊙P与⊙O外切于点B,与直线CD相切于点E,设⊙O与⊙P的半径分别为r与R,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com