
【题目】如图,AB=AC,∠CAB=90°,∠ADC=45°,AD=1,CD=3,则BD的长为( )
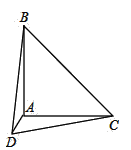
A.3B.![]() C.2
C.2![]() D.4
D.4
科目:初中数学 来源: 题型:
【题目】已知,如图,点A、D、B、E在同一直线上,AC=EF,AD=BE,∠A=∠E,
(1)求证:△ABC≌△EDF;
(2)当∠CHD=120°,猜想△HDB的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:![]() ≈2.449,结果保留整数)
≈2.449,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a=2 002x+2 003,b=2 002x+2 004,c=2 002x+2 005,则多项式a2+b2+c2-ab-bc-ca的值为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300![]() 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),

(1)求围栏的长和宽;
(2)能否围成面积为400 ![]() 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=![]() x+2与x轴交于点A,与y轴交于点B,直线l2:y=-2x+b经过点B且与x轴交于点C.
x+2与x轴交于点A,与y轴交于点B,直线l2:y=-2x+b经过点B且与x轴交于点C.
(1)b=________;(答案直接填写在答题卡的横线上)
(2)画出直线l2的图象;
(3)求△ABC的面积
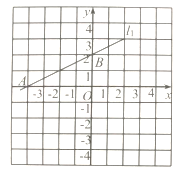
查看答案和解析>>
科目:初中数学 来源: 题型:
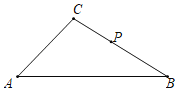
【题目】如图,点C,D在线段AB上,△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图①,在△ABC 中,D、E 分别是 AB、AC 上的点,AB=AC,AD=AE,然后将△ADE 绕点 A 顺时针旋转一定角度,连接 BD,CE,得到图②,将 BD、CE 分别延长至 M、N,使 DM=![]() BD,EN=
BD,EN=![]() CE,得到图③,请解答下列问题:
CE,得到图③,请解答下列问题:
(1)在图②中,BD 与 CE 的数量关系是 ;
(2)在图③中,猜想 AM 与 AN 的数量关系,∠MAN 与∠BAC 的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知a为正整数,关于x的不等式组![]() 的整数解仅2、3、4,则a的最大值是_____.
的整数解仅2、3、4,则a的最大值是_____.
(2)如图,△ABC中,AC=![]() ,∠A=45°,∠B=30°,P是BC边上一点(不含端点),将PC绕着点P逆时针旋转得到PC′,旋转角α(0<α<180°),若旋转过程中,点C′始终落在△ABC内部(不包含边上),则PC的取值范围是_____.
,∠A=45°,∠B=30°,P是BC边上一点(不含端点),将PC绕着点P逆时针旋转得到PC′,旋转角α(0<α<180°),若旋转过程中,点C′始终落在△ABC内部(不包含边上),则PC的取值范围是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com