【题目】如图，点C，D在线段AB上，△PCD是等边三角形．
(1)当AC，CD，DB满足怎样的关系时，△ACP∽△PDB?
(2)当△ACP∽△PDB时，求∠APB的度数．
【答案】(1) CD2＝AC·DB时，△ACP∽△PDB.
(2) 120°.
【解析】试题分析：（1）由△PCD是等边三角形可得∠ACP＝∠PDB＝120°，当
＝
，即
＝
,即当CD2＝AC·DB时，△ACP∽△PDB；（2）由△ACP∽△PDB可得∠A＝∠DPB，所以∠APB＝∠APC＋∠CPD＋∠DPB＝∠APC＋∠CPD＋∠A＝∠PCD＋∠CPD＝120°.
试题解析：
(1)∵△PCD是等边三角形，
∴∠ACP＝∠PDB＝120°.
当
＝
，即
＝
,即当CD2＝AC·DB时，△ACP∽△PDB.
(2)∵△ACP∽△PDB，∴∠A＝∠DPB.
∴∠APB＝∠APC＋∠CPD＋∠DPB＝∠APC＋∠CPD＋∠A＝∠PCD＋∠CPD＝120°.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】在2018年“新技术支持未来教育”的教师培训活动中，会议就“面向未来的学校教育、家庭教育及实践应用演示”等问题进行了互动交流，记者随机采访了部分参会教师，对他们发言的次数进行了统计，并绘制了不完整的统计表和条形统计图．
组别 | 发言次数n | 百分比 |
A | 0≤n＜3 | 10% |
B | 3≤n＜6 | 20% |
C | 6≤n＜9 | 25% |
D | 9≤n＜12 | 30% |
E | 12≤n＜15 | 10% |
F | 15≤n＜18 | m% |
请你根据所给的相关信息，解答下列问题：
（1）本次共随机采访了 _____ 名教师，m= _____ ；
（2）补全条形统计图；
（3）已知受访的教师中，E组只有2名女教师，F组恰有1名男教师，现要从E组、F组中分别选派1名教师写总结报告，请用列表法或画树状图的方法，求所选派的两名教师恰好是1男1女的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知AP是△ABC的外角平分线，连结PB、PC．
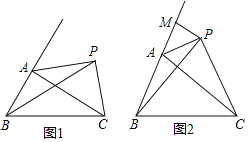
（1）如图1①若BP平分∠ABC，且∠ACB＝28°，求∠APB的度数．
②若P与A不重合，请判断AB+AC与PB+PC的大小关系，并证明你的结论．
（2）如图2，若过点P作PM⊥BA，交BA的延长线于M点，且∠BPC＝∠BAC，求：
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠BAC=90°，AB=4，AC=3，DE垂直平分AB，分别交AB、BC于点D、E，AP平分∠BAC，与DE的延长线交于点P．
（1）求PD的长度；
（2）连结PC，求PC的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义一种新运算“”：观察下列各式：
23＝2×3+3＝9；3（﹣1）＝3×3﹣1＝8；
44＝4×3+4＝16：5（﹣3）＝5×3﹣3＝12
（1）请你想一想：ab＝ ；
（2）已知（a+3）2与|b﹣1|互为相反数，c与a互为倒数，试求c（ab）的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
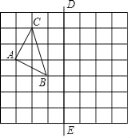
【题目】如图，在所给的网格图中，完成下列各题（用直尺画图，否则不给分）
（1）画出格点△ABC关于直线DE的对称的△A1B1C1；
（2）在DE上画出点P，使PA+PC最小；
（3）在DE上画出点Q，使QA﹣QB最大．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
