
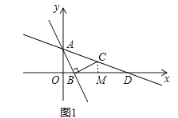
【题目】如图1,一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作线段
作线段![]() 且
且![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)点![]() 的坐标轴__________,点
的坐标轴__________,点![]() 的坐标轴__________;
的坐标轴__________;
(2)直接写出点![]() 的坐标轴__________,并求出直线
的坐标轴__________,并求出直线![]() 的函数关系式;
的函数关系式;
(3)若点![]() 是图1中直线
是图1中直线![]() 上的一点,连接
上的一点,连接![]() ,得到图2,当点
,得到图2,当点![]() 在第二象限,且到
在第二象限,且到![]() 轴,
轴,![]() 轴的距离相等时,直接写出
轴的距离相等时,直接写出![]() 的面积;
的面积;
(4)若点![]() 是图1中坐标平面内不同于点
是图1中坐标平面内不同于点![]() 、点
、点![]() 的一点,当以点
的一点,当以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等时,直接写出点
全等时,直接写出点![]() 的坐标.
的坐标.

【答案】(1)![]()
![]() ;(2)
;(2)![]() ,
,![]() ;(3)3;(4)
;(3)3;(4)![]() 或
或![]() 或
或![]()
【解析】
(1)将x=0和y=0分别代入一次函数解析式中,即可分别求出点A、B的坐标;
(2)过点C作CM⊥x轴于M,利用AAS证出△AOB≌△BMC,从而得出OB=CM=1,OA=MB=2,即可求出点C的坐标,然后设直线AC的解析式为y=kx+b,将点A、C的坐标代入即可求出该解析式;
(3)过点P作PN⊥y轴于点N,根据题意可设点P的坐标为(-a, a),将点P代入直线AC的解析式中即可求出点P的坐标,从而求出PN的长,然后根据三角形的面积公式计算即可;
(4)先求出点D的坐标,然后根据点Q的位置和全等三角形的对应情况分类讨论,分别画出对应的图形,根据全等三角形的性质、等腰直角三角形的性质和平移规律分别求点Q的坐标即可.
解:(1)∵一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
∴当x=0时,解得y=2;当y=0时,解得x=1
∴点A的坐标为(0,2),点B的坐标为(1,0)
故答案为:(0,2);(1,0);
(2)过点C作CM⊥x轴于M
∴∠AOB=∠BMC=∠ABC=90°
∴∠OAB+∠ABO=90°,∠MBC+∠ABO=180°-∠ABC=90°
∴∠OAB=∠MBC
在△AOB和△BMC中
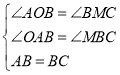
∴△AOB≌△BMC
∴OB=CM=1,OA=MB=2
∴OM=OB+MB=3
∴点C的坐标为(3,1)
故答案为:(3,1);
设直线AC的解析式为y=kx+b
将A、C两点的坐标代入,得
![]()
解得: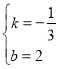
∴直线AC的解析式为![]()
(3)过点P作PN⊥y轴于点N
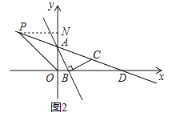
∵点![]() 在第二象限,且到
在第二象限,且到![]() 轴,
轴,![]() 轴的距离相等
轴的距离相等
可设点P的坐标为(-a, a)
将点P的坐标代入直线AC的解析式中,得
![]()
解得:![]()
∴点P的坐标为(-3,3)
∴PN=3
∴S△AOP=![]() OA·PN=
OA·PN=![]() ×2×3=3
×2×3=3
(4)将y=0代入直线AC的解析式中,解得x=6
∴点D的坐标为(6,0)
①当点Q在直线AC的上方,且△QDC≌△BCD时,如下图所示
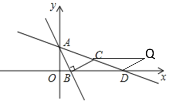
∴∠BDC=∠QCD,CQ=BD=6-1=5
∴CQ∥x轴
∴点Q可看成由点C向右平移5个单位长度
∴此时点Q的坐标为(8,1);
②当点Q在直线AC的上方,且△QCD≌△BCD时,如下图所示
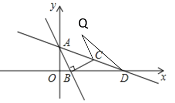
∴QC = BC,∠QCD=∠BCD
∴∠QCA=∠BCA
∵∠ABC=90°,BA=BC
∴△ABC为等腰直角三角形,QC=BA
∴∠BAC=∠BCA=∠QCA=45°
∴QC∥AB
∴QC可看成AB平移得出
∵点B(1,0)到点C(3,1)的平移方式为:先向右平移2个单位,再向上平移1个单位
∴点Q是由点A(0,2)先向右平移2个单位,再向上平移1个单位
∴此时点Q的坐标为(2,3);
③当点Q在直线AC的下方,且△QDC≌△BCD时,如下图所示
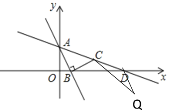
∴QD=BC,∠QDC=∠BCD
∵∠ABC=90°,BA=BC
∴△ABC为等腰直角三角形,QD=BA
∴∠BAC=∠BCA =45°,
∴∠BCD=180°-∠BCA=135°
∴∠QDC=135°
∴∠QDC+∠BAC=180°
∴QD∥BA
∴QD可看成BA平移得出
∵点A(0,2)到点D(6,0)的平移方式为:先向右平移6个单位,再向下平移2个单位
∴点Q是由点B(1,0)先向右平移6个单位,再向下平移2个单位
∴此时点Q的坐标为(7,-2);
④当点Q在直线AC的下方,且△QCD≌△BCD时,此时点Q与点B重合,不符合题意,舍去.
综上所述:点Q的坐标为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
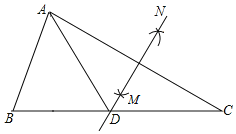
【题目】如图在△ABC中,∠B=50°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,
(1)若△ABD的周长是19,AB=7,求BC的长;
(2)求∠BAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD(正方形四边相等,四个角均为直角)中,AB=8,P为线段BC上一点,连接AP,过点B作BQ⊥AP,交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交AD于点N.
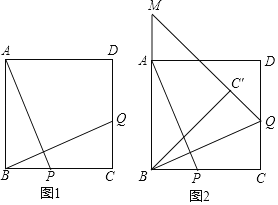
(1)求证:BP=CQ;
(2)若BP=![]() PC,求AN的长;
PC,求AN的长;
(3)如图2,延长QN交BA的延长线于点M,若BP=x(0<x<8),△BMC'的面积为S,求S与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
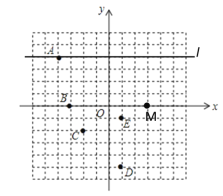
【题目】在平面直角坐标系中,每个小方格的边长为一个单位长度.
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________;
的坐标为__________;
(2)点![]() 关于
关于![]() 轴对称点的坐标为__________;
轴对称点的坐标为__________;
(3)在直线![]() 上找一点
上找一点![]() ,使
,使![]() 为等腰三角形,点
为等腰三角形,点![]() 坐标为__________
坐标为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
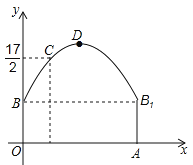
【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
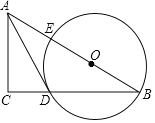
【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B.
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com