
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是直线
是直线![]() 上一点,把
上一点,把![]() 沿
沿![]() 所在的直线翻折后,点
所在的直线翻折后,点![]() 落在直线
落在直线![]() 上的点
上的点![]() 处,
处,![]() 的长是__________
的长是__________

【答案】![]() 或
或![]()
【解析】
根据折叠后点C的对应点H与AC的位置关系分类讨论,分别画出对应的图形,利用勾股定理求出各边的长,再根据折叠的性质与勾股定理列出对应的方程即可求出结论.
解:①当折叠后点C的对应点H在AC的下方时,如下图所示

∵![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
根据勾股定理可得BC=![]()
∵![]() ,
,![]() ,
,
∴![]()
![]() ,
,![]()
![]()
∵![]()
根据勾股定理可得DE=![]()
由折叠的性质可得:DH=CD=![]() ,CP=PH
,CP=PH
∴EH=DH-DE=![]()
设CP=PH=x,则EP=CE-CP=![]() -x
-x
在Rt△PEH中,EP2+EH2=PH2
即(![]() -x)2+(
-x)2+(![]() )2=x2
)2=x2
解得:x=![]()
即此时CP=![]() ;
;
②当折叠后点C的对应点H在AC的上方时,如下图所示

根据折叠的性质可得DH=CD=![]() ,CP=PH
,CP=PH
∴EH=DH+DE=![]()
设CP=PH=y,则EP= CP-CE =y-![]()
在Rt△PEH中,EP2+EH2=PH2
即(y-![]() )2+(
)2+(![]() )2=y2
)2=y2
解得:y=![]()
即此时CP=![]() .
.
综上所述:CP=![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AB上,点E在边AC的左侧,连接AE.
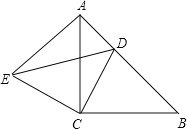
(1)求证:AE=BD;
(2)试探究线段AD、BD与CD之间的数量关系;
(3)过点C作CF⊥DE交AB于点F,若BD:AF=1:2![]() ,CD=
,CD=![]() ,求线段AB的长.
,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A、B,与y轴交于点C,且OA=1,OB=3,顶点为D,对称轴交x轴于点Q.
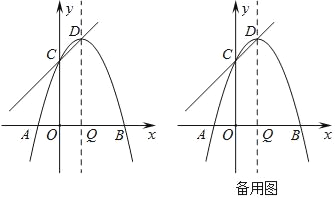
(1)求抛物线对应的二次函数的表达式;
(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(3)在抛物线的对称轴上是否存在一点M,使得△DCM∽△BQC?如果存在,求出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
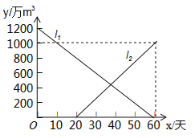
【题目】今年夏天,重庆各区持续高温日数达到历史之最,受持续高温和连日无雨的影响,重庆某水库的蓄水量随时间的增加而减少,己知原有蓄水量![]() (万
(万![]() )与干旱持续时间
)与干旱持续时间![]() (天)的关系如图中线段
(天)的关系如图中线段![]() 所示,针对这种干旱情况,从第20天开始向水库注水,注水量
所示,针对这种干旱情况,从第20天开始向水库注水,注水量![]() (万
(万![]() )与时间
)与时间![]() (天)的关系如图中线段
(天)的关系如图中线段![]() 所示(不考虑其他因素).若总蓄水量不多于900万
所示(不考虑其他因素).若总蓄水量不多于900万![]() 为严重干早,则该水库发生严重干旱共__________天
为严重干早,则该水库发生严重干旱共__________天
查看答案和解析>>
科目:初中数学 来源: 题型:
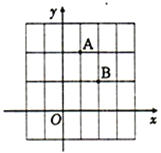
【题目】点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是![]() 轴上使得∣PA—PB∣的值最大的点,Q是
轴上使得∣PA—PB∣的值最大的点,Q是![]() 轴上使得QA+QB的值最小的点,则OP·OQ=__________.
轴上使得QA+QB的值最小的点,则OP·OQ=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作线段
作线段![]() 且
且![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)点![]() 的坐标轴__________,点
的坐标轴__________,点![]() 的坐标轴__________;
的坐标轴__________;
(2)直接写出点![]() 的坐标轴__________,并求出直线
的坐标轴__________,并求出直线![]() 的函数关系式;
的函数关系式;
(3)若点![]() 是图1中直线
是图1中直线![]() 上的一点,连接
上的一点,连接![]() ,得到图2,当点
,得到图2,当点![]() 在第二象限,且到
在第二象限,且到![]() 轴,
轴,![]() 轴的距离相等时,直接写出
轴的距离相等时,直接写出![]() 的面积;
的面积;
(4)若点![]() 是图1中坐标平面内不同于点
是图1中坐标平面内不同于点![]() 、点
、点![]() 的一点,当以点
的一点,当以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等时,直接写出点
全等时,直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
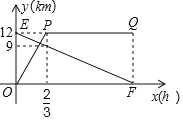
【题目】甲骑自行车从![]() 地出发前往
地出发前往![]() 地,同时乙步行从
地,同时乙步行从![]() 地出发前往
地出发前往![]() 地,如图的折线
地,如图的折线![]() 和线段
和线段![]() ,分别表示甲、乙两人与
,分别表示甲、乙两人与![]() 地的距离
地的距离![]() 甲 ,
甲 ,![]() 乙与他们所行时间
乙与他们所行时间![]() 之间的函数关系.
之间的函数关系.
(1)求线段![]() 对应的
对应的![]() 甲与
甲与![]() 的函数关系式并注明自变量
的函数关系式并注明自变量![]() 的取值范围;
的取值范围;
(2)求![]() 乙与
乙与![]() 的函数关系式及乙到达
的函数关系式及乙到达![]() 地所用的时间;
地所用的时间;
(3)经过 小时,甲、乙两人相距![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:弦切角:顶点在圆上,一边与圆相交,另一边和圆相切的角叫弦切角.
问题情景:已知如图所示,直线![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,
,![]() 为
为![]() 的一条弦,
的一条弦,![]() 为弧
为弧![]() 所对的圆周角.
所对的圆周角.
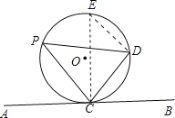
(1)猜想:弦切角![]() 与
与![]() 之间的关系.试用转化的思想:即连接
之间的关系.试用转化的思想:即连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,来论证你的猜想.
,来论证你的猜想.
(2)用自己的语言叙述你猜想得到的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com