
【题目】(1)如图1,在△ABC中,∠ACB是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F,
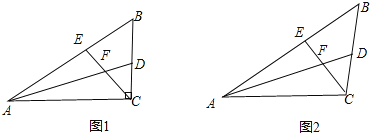
①请你猜想写出FE与FD之间的数量关系,不用说明理由;
②判断∠AFC与∠B的数量关系,请说明理由.
(2)如图2,在△ABC中,如果∠ACB不是直角,而(1)中其他条件不变,请问你在(1)中所得FE与FD之间的数量关系是否依然成立?请说明理由.
【答案】(1)①FE=FD;②∠AFC=2∠B;(2)FE=FD仍然成立,理由见解析.
【解析】
(1)①首先过点F作FM⊥BC于M.作FN⊥AB于N,连接BF,根据角平分线的性质,可得FM=FN,又由在Rt△ABC中,∠ACB=90°,∠B=60°,求得∠NEF=75°=∠MDF,又由∠DMF=∠ENF=90°,利用AAS,即可证得△DMF≌△ENF,由全等三角形的对应边相等,即可证得FE=FD;②由①知∠BCE=45°,∠CDF=75°,利用三角形的外角等于与它不相邻两个内角的和,可求出.(2)过点F作FM⊥BC于M.作FN⊥AB于N,连接BF,根据角平分线的性质,可得FN=FM,由∠ABC=60°,即可求得∠MFN=120°,∠EFD=∠AFC=120°,继而求得∠DFM=∠NFE,利用ASA,即可证得△DMF≌△ENF,由全等三角形的对应边相等,即可证得FE=FD.
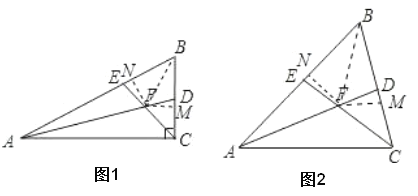
(1)①如图1,过点F作FM⊥BC于M.作FN⊥AB于N,连接BF,
∵F是角平分线交点,
∴BF也是角平分线,
∴MF=FN,∠DMF=∠ENF=90°,
∵在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠DAC= ![]() ∠BAC=15°,
∠BAC=15°,
∴∠CDA=75°,
∵∠MFC=45°,∠MFN=120°,
∴∠NFE=15°,
∴∠NEF=75°=∠MDF,
在△DMF和△ENF中,
∠DMF=∠ENF,∠MDF=∠NEF,MF=NF,
∴△DMF≌△ENF(AAS),
∴FE=FD;
②由①知∠BCE=45°,∠CDF=75°,所以∠AFC=120°,因为∠B=60°,所以∠AFC=2∠B.
(2)如图2,过点F作FM⊥BC于M.作FN⊥AB于N,连接BF,
∵F是角平分线交点,
∴BF也是角平分线,
∴MF=FN,∠DMF=∠ENF=90°,
∴四边形BNFM是圆内接四边形,
∵∠ABC=60°,
∴∠MFN=180°-∠ABC=120°,
∵∠CFA=180°-(∠FAC+∠FCA)=180°- ![]() (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°- ![]() (180°-∠ABC)=180°-
(180°-∠ABC)=180°- ![]() (180°-60°)=120°,
(180°-60°)=120°,
∴∠DFE=∠CFA=∠MFN=120°.
又∵∠MFN=∠MFD+∠DFN,∠DFE=∠DFN+∠NFE,
∴∠DFM=∠NFE,
在△DMF和△ENF中,
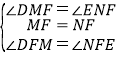
∴△DMF≌△ENF(ASA),
∴FE=FD.


科目:初中数学 来源: 题型:
【题目】芜湖国际动漫节期间,小明进行了富有创意的形象设计.如图1,他在边长为1的正方形ABCD内作等边三角形BCE,并与正方形的对角线交于F、G点,制成如图2的图标.则图标中阴影部分图形AFEGD的面积=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆汽车在直线形的公路上由A向B行驶,M,N分别是位于AB两侧的村庄.

(1)设汽车行驶到公路AB上点P的位置时,距离村庄M最近,行驶到点Q的位置时,距离村庄N最近,在图中的公路AB上分别画出点P,Q位置.
(2)在公路AB上是否存在这样一点H,使汽车行驶到该点时,与村庄M,N的距离相等?如果存在请在图中AB上画出这一点,如果不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=![]() x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
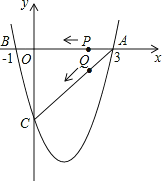
(1)求该二次函数的解析式及点C的坐标;
(2)当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E,使得以A,E,Q为顶点的三角形为等腰三角形?若存在,请求出E点坐标;若不存在,请说明理由.
(3)当P,Q运动到t秒时,△APQ沿PQ翻折,点A恰好落在抛物线上D点处,请判定此时四边形APDQ的形状,并求出D点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学玩转盘游戏时,把质地相同的两个盘A、B分别平均分成2份和3份,并在每一份内标有数字如图.游戏规则:甲、乙两同学分别同时转动两个转盘各1次,当转盘停止后,指针所在区域的数字之积为偶数时甲胜;数字之积为奇数时乙胜.若指针恰好在分割线上,则需要重新转动转盘.
(1)用树状图或列表的方法,求甲获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗?请判断并说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2(m+1)x+m2+2=0
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2,且满足x12+x22=10,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD内两点M、N,满足MB⊥BC,MD⊥DC,NB⊥BA,ND⊥DA,若四边形BMDN的面积是菱形ABCD面积的![]() ,则cosA= ______ .
,则cosA= ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中表示下面各点:
A(0,3);B(1,-3);C(3,-5);D(-3,-5);E(3,5);F(5,7);G(5,0)
(1)A点到原点O的距离是 。
(2)将点C向![]() 轴的负方向平移6个单位,它与点 重合。
轴的负方向平移6个单位,它与点 重合。
(3)连接CE,则直线CE与![]() 轴是什么关系?
轴是什么关系?
(4)点F分别到![]() 、
、![]() 轴的距离是多少?
轴的距离是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com