
 如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.分析 (1)根据网格结构找出点B、C关于直线l的对称点B′、C′的位置,然后与点A顺次连接即可;
(2)利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解;
(3)根据轴对称确定最短路线问题,连接B′C与直线l的交点即为所求点P.
解答 解:(1)△AB′C′如图所示;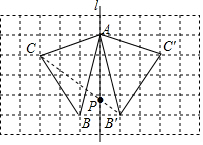
(2)△ABC的面积=3×4-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×4-$\frac{1}{2}$×1×3,
=12-3-2-1.5,
=12-6.5,
=5.5;
(3)点P如图所示.
点评 本题考查了利用轴对称确定最短路线问题,利用轴对称变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
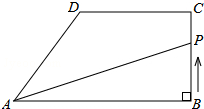 如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC在平面直角坐标系中的位置如图所示:
△ABC在平面直角坐标系中的位置如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,过D作⊙O切线DE交AC于点E.
如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,过D作⊙O切线DE交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
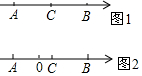 如图1,在数轴上,A点、B点与C点的距离相等.
如图1,在数轴上,A点、B点与C点的距离相等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com