
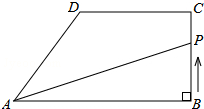
 如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).分析 (1)当t=3时,可求出P运动的路程即BP的长,再根据三角形的面积公式计算即可;
(2)当点P在DA上运动时,过D作DH⊥AB,P′M⊥AB,求出P′M的值即为△PAB中AB边上的高,再利用三角形的面积公式计算即可;
(3)当S=12时,则P在BC或AD上运动,利用(1)和(2)中的面积和高的关系求出此时的t即可.
解答 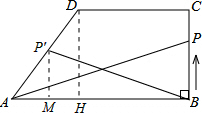 解:(1)∵动点P以1cm/s的速度运动,
解:(1)∵动点P以1cm/s的速度运动,
∴当t=3时,BP=3cm,
∴S=$\frac{1}{2}$AB•BP=$\frac{1}{2}$×8×3=12(cm2);
(2)过D作DH⊥AB,过P′作P′M⊥AB,
∴P′M∥DH,
∴△AP′M∽△ADH,
∴$\frac{AP′}{AD}$=$\frac{PM}{DH}$,
∵AB=8cm,CD=5cm,
∴AH=AB-DC=3cm,
∵BC=4cm,
∴AD=$\sqrt{{3}^{2}+{4}^{2}}$=5cm,
又∵A′P=14-t,
∴$\frac{14-t}{5}$,
∴P′M=$\frac{4(14-t)}{5}$,
∴S=$\frac{1}{2}$AB•P′M=$\frac{16(14-t)}{5}$,
即S关于t的函数表达式S=$\frac{16(14-t)}{5}$;
(3)由题意可知当P在CD上运动时,S=$\frac{1}{2}$AB×BC=$\frac{1}{2}$×8×4=16cm2,
所以当S=12时,P在BC或AD上,
当P在BC上时,12=$\frac{1}{2}$×8•t,解得:t=3;
当P在AD上时,12=$\frac{16(14-t)}{5}$,解得:t=$\frac{41}{4}$.
∴当S=12时,t的值为3或$\frac{41}{4}$.
点评 本题考查了直角梯形的性质、相似三角形的判定和性质以及勾股定理的运用和三角形面积公式的运用,题目的综合性较强,难度中等,对于动点问题特别要注意的是分类讨论数学思想的运用.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
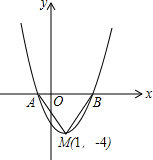 如图是二次函数y=(x-1)2-4的图象,与x轴交于A,B两点.将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围.
如图是二次函数y=(x-1)2-4的图象,与x轴交于A,B两点.将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 A、B、C、D四位同事去茶馆喝茶,现A已入坐,B、C、D三人将随机坐到其余三个位置上.若A希望与D相邻而坐,那么他实现愿望的概率为多少?(要求画树状图列出所有的可能情况)
A、B、C、D四位同事去茶馆喝茶,现A已入坐,B、C、D三人将随机坐到其余三个位置上.若A希望与D相邻而坐,那么他实现愿望的概率为多少?(要求画树状图列出所有的可能情况)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com