
| 射击成绩(环) | 6 | 7 | 8 | 9 | 10 |
| 甲射击频数 | 0 | 3 | 4 | 3 | 0 |
| 乙射击频数 | 1 | 3 | 2 | 3 | 1 |
分析 (1)根据众数的概念确定甲、乙射击成绩的众数;
(2)根据加权平均数的计算公式求出甲、乙的平均射击成绩;
(3)根据方差的计算公式求出甲、乙两名运动员的射击成绩的方差,根据方差的意义比较得到答案.
解答 解:(1)甲射击成绩的众数是8,
乙射击成绩的众数是7和9;
(2)甲的平均射击成绩为:$\frac{1}{10}$(7×3+8×4+9×3)=8,
乙的平均射击成绩为:$\frac{1}{10}$(6×1+7×3+8×2+9×3+10×1)=8;
(3)甲的波动大,理由如下:
甲的方差为:$\frac{1}{10}$[(7-8)2+(7-8)2+(7-8)2+(8-8)2+(8-8)2+(8-8)2+(8-8)2+(9-8)2+(9-8)2+(9-8)2]=0.6,
乙的方差为:$\frac{1}{10}$[(6-8)2+(7-8)2+(7-8)2+(7-8)2+(8-8)2+(8-8)2+(9-8)2+(9-8)2+(9-8)2+(10-8)2]=1.4,
∵0.6<1.4,
∴甲的波动大.
点评 本题考查的是众数的概念、加权平均数的计算和方差的计算和意义,掌握众数的概念、加权平均数的计算公式和方差的计算公式是解题的关键.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:选择题
| A. | 有且只有一条直线垂直于已知直线 | |
| B. | 从直线外一点到这条直线的垂线段,叫做这点到这条直线距离 | |
| C. | 不相交的两条线段一定平行 | |
| D. | 直线c外一点A与直线c上各点连接而成的所有线段中最短线段的长是3cm,则点A到直线c的距离是3cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
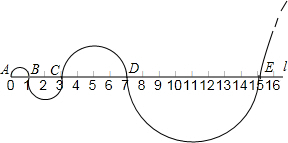 如图,在你标有刻度的直线l上,从点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆…,按此规律,则第4个半圆的面积是第3个半圆面积的4倍,第n个半圆的面积为22n-5π.(结果保留π)
如图,在你标有刻度的直线l上,从点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆…,按此规律,则第4个半圆的面积是第3个半圆面积的4倍,第n个半圆的面积为22n-5π.(结果保留π)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com