【题目】已知O为直线AB上的一点，∠COE是直角，OF平分∠AOE.

（1）如图①，若∠COF＝34°，则∠BOE＝________；若∠COF＝m°，则∠BOE＝________，∠BOE与∠COF的数量关系式为________；

（2）当射线OE绕点O逆时针旋转到如图②的位置时，（1）中∠BOE与∠COF的数量关系是否成立？请说明理由．

参考答案：

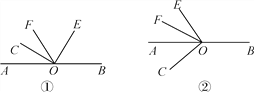
【答案】（1）68°，2m°，∠BOE＝2∠COF；（2）成立，理由见解析.

【解析】（1）由∠COF=34°，∠COE是直角，易求∠EOF，而OE平分∠AOE，可求∠AOE，进而可求∠BOE，若∠COF=m°，则∠BOE=2m°；进而可知∠BOE=2∠COF；
（2）由于∠COE是直角，于是∠EOF=90°-∠COF，而OF平分∠AOE，则有∠AOE=2∠EOF，从而可得∠BOE=180°-∠AOE=180°-2（90°-∠COF）=2∠COF．

解：（1）∵∠COF=34°，∠COE是直角，
∴∠EOF=90°-34°=56°，
又∵OF平分∠AOE，
∴∠AOE=2∠EOF=112°，
∴∠BOE=180°-112°=68°，
若∠COF=m°，则∠BOE=2m°；
故∠BOE=2∠COF；
故答案是68°；2m°；∠BOE=2∠COF；
（2）∠BOE和∠COF的关系依然成立．
∵∠COE是直角，
∴∠EOF=90°-∠COF，
又∵OF平分∠AOE，
∴∠AOE=2∠EOF，
∴∠BOE=180°-∠AOE=180°-2（90°-∠COF）=2∠COF．

“点睛”本题考查了角的计算．解题的关键是注意找出所求角与已知角之间的关系，例如：互余、互补关系．

关闭