
ЁОЬтФПЁПдФЖСВФСЯЃК
ЙигкШ§НЧКЏЪ§ЛЙгаШчЯТЕФЙЋЪНЃК
Sin(ІС![]() ІТ)=sinІСcosІТ
ІТ)=sinІСcosІТ![]() cosІСsinІТ
cosІСsinІТ
tan(ІС![]() ІТ)=
ІТ)=![]()
РћгУетаЉЙЋЪНПЩвдНЋвЛаЉВЛЪЧЬиЪтНЧЕФШ§НЧКЏЪ§зЊЛЏЮЊЬиЪтНЧЕФШ§НЧКЏЪ§РДЧѓжЕЃЌ
Р§ЃКtan15Ёу=tan(45Ёу-30Ёу)
=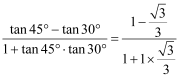
=![]()
=![]()
ИљОнвдЩЯдФЖСВФСЯЃЌЧыбЁдёЪЪЕБЕФЙЋЪННтД№ЯТУцЕФЮЪЬт
ЃЈ1ЃЉМЦЫуsin15Ёу
ЃЈ2ЃЉЮвЯиЬхг§ГЁгавЛвЦЖЏЙЋЫОЕФаХКХЫўЃЌаЁУїЯыРћгУЫљбЇЕФЪ§бЇжЊЪЖРДВтСПИУЫўЕФИпЖШЃЌаЁЛЊеОдкРыЫўЕзAОрРы7УзЕФCДІЃЌВтЕУЫўЖЅЕФбіНЧЮЊ75ЁуЃЌаЁЛЊЕФблОІРыЕиУцЕФОрРыDCЮЊ1.62УзЃЌЧыАяжњаЁЛЊЧѓГіИУаХКХЫўЕФИпЖШЁЃЃЈОЋШЗЕН0.1УзЃЌВЮПМЪ§ОнЃК![]() ЃЉ
ЃЉ
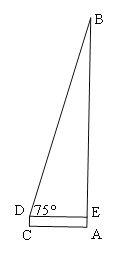
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉдМЮЊ27.7УзЃЎ
ЃЛЃЈ2ЃЉдМЮЊ27.7УзЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉАб15ЁуЛЏЮЊ45Ёу-30ЁувдКѓЃЌдйРћгУЙЋЪНsinЃЈІСЁРІТЃЉ=sinІСcosІТЁРcosasinІТМЦЫуЃЌМДПЩЧѓГіsin15ЁуЕФжЕЃЛ
ЃЈ2ЃЉЯШИљОнШёНЧШ§НЧКЏЪ§ЕФЖЈвхЧѓГіBEЕФГЄЃЌдйИљОнAB=AE+BEМДПЩЕУГіНсТлЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉsin15Ёу=sinЃЈ45Ёу-30ЁуЃЉ=sin45Ёуcos30Ёу-cos45Ёуsin30Ёу=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкRtЁїBDEжаЃЌЁпЁЯBED=90ЁуЃЌЁЯBDE=75ЁуЃЌDE=AC=7УзЃЌ
ЁрBE=DEЁСtanЁЯBDE=DEЁСtan75ЁуЃЎ
Ёпtan75Ёу=tanЃЈ45Ёу+30ЁуЃЉ=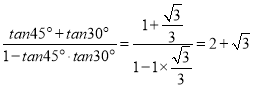 ЃЌ
ЃЌ
ЁрBE=7ЃЈ2+![]() ЃЉ=14+7
ЃЉ=14+7![]() ЃЌ
ЃЌ
ЁрAB=AE+BE=1.62+14+7![]() Ёж27.7ЃЈУзЃЉЃЎ
Ёж27.7ЃЈУзЃЉЃЎ
Д№ЃКаХКХЫўЕФИпЖШдМЮЊ27.7УзЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖрЯюЪНЉ3x2+mx+nx2+x+3ЕФжЕгыxЕФШЁжЕЮоЙиЃЌЧѓДњЪ§ЪНmnЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁЯІСгыЁЯІТЛЅгрЃЌЧвЁЯІС=35Ёу18ЃЌЃЌдђЁЯІТ=________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЫФБпаЮABCDЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
AЃЎЕБAD=BCЃЌABЁЮDCЪБЃЌЫФБпаЮABCDЪЧЦНааЫФБпаЮ
BЃЎЕБAD=BCЃЌAB=DCЪБЃЌЫФБпаЮABCDЪЧЦНааЫФБпаЮ
CЃЎЕБAC=BDЃЌACЦНЗжBDЪБЃЌЫФБпаЮABCDЪЧОиаЮ
DЃЎЕБAC=BDЃЌACЁЭBDЪБЃЌЫФБпаЮABCDЪЧе§ЗНаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтжаЃЌецУќЬтЪЧЃЈ ЃЉ
AЃЎЖдНЧЯпЯрЕШЕФЫФБпаЮЪЧОиаЮ
BЃЎЖдНЧЯпЛЅЯрДЙжБЕФЫФБпаЮЪЧСтаЮ
CЃЎЖдНЧЯпЛЅЯрЦНЗжЕФЫФБпаЮЪЧЦНааЫФБпаЮ
DЃЎЖдНЧЯпЛЅЯрДЙжБЦНЗжЕФЫФБпаЮЪЧе§ЗНаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћгЏРћ15дЊМЧзї+15ЃЌФЧУДПїБО51дЊМЧзїЃЈ ЃЉ
A.+51дЊ
B.Љ51дЊ
C.+15дЊ
D.Љ15
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=Ѓ![]() +
+![]() +4ЕФЭМЯѓгыyжсНЛгкЕуAЃЌгыxжсНЛгкBЁЂCСНЕуЃЌЦфЖдГЦжсгыxжсНЛгкЕуDЃЌСЌНгACЃЎ
+4ЕФЭМЯѓгыyжсНЛгкЕуAЃЌгыxжсНЛгкBЁЂCСНЕуЃЌЦфЖдГЦжсгыxжсНЛгкЕуDЃЌСЌНгACЃЎ
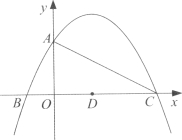
(1)ЕуAЕФзјБъЮЊ_______ ЃЌЕуCЕФзјБъЮЊ_______ ЃЛ
(2)ЯпЖЮACЩЯЪЧЗёДцдкЕуEЃЌЪЙЕУЁїEDCЮЊЕШбќШ§НЧаЮ?ШєДцдкЃЌЧѓГіЫљгаЗћКЯЬѕМўЕФЕуEЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
(3)ЕуPЮЊxжсЩЯЗНЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌСЌНгPAЁЂPCЃЌШєЫљЕУЁїPACЕФУцЛ§ЮЊSЃЌдђSШЁКЮжЕЪБЃЌЯргІЕФЕуPгаЧвжЛга2Иі?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩЯЮч9Еу30ЗжЪБЃЌЪБеыгыЗжеыГЩ___________ЖШЁЃЃЈШЁаЁгк180ЖШЕФНЧЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊOЪЧПкABCDЖдНЧЯпЕФНЛЕуЃЌЁїABCЕФУцЛ§ЪЧ3ЃЌдђПкABCDЕФУцЛ§ЪЧЃЈ ЃЉ
AЃЎ3 BЃЎ6 CЃЎ9 DЃЎ12
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com