
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
【答案】
(1)证明:∵PQ垂直平分BE,
∴QB=QE,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,
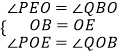 ,
,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵QB=QE,
∴四边形BPEQ是菱形;
(2)解:∵O,F分别为PQ,AB的中点,
∴AE+BE=2OF+2OB=18,
设AE=x,则BE=18﹣x,
在Rt△ABE中,62+x2=(18﹣x)2,
解得x=8,
BE=18﹣x=10,
∴OB= ![]() BE=5,
BE=5,
设PE=y,则AP=8﹣y,BP=PE=y,
在Rt△ABP中,62+(8﹣y)2=y2,解得y= ![]() ,
,
在Rt△BOP中,PO= ![]() =
= ![]() ,
,
∴PQ=2PO= ![]() .
.
【解析】(1)先根据线段垂直平分线的性质证明QB=QE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形ABGE是平行四边形,得到QB=QE,再根据菱形的判定即可得出四边形BPEQ是菱形;
(2)根据三角形中位线的性质可得AE+BE=2OF+2OB=18,设AE=x,则BE=18-x,在Rt△ABE中,根据勾股定理可得62+x2=(18-x)2,BE=10,得到OB=5,再勾股定理求出y和PO的值即可PQ的长.
【考点精析】通过灵活运用线段垂直平分线的性质和矩形的性质,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;矩形的四个角都是直角,矩形的对角线相等即可以解答此题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】如图,∠ABC的两边分别与∠DEF的两边平行,即BA∥ED,BC∥EF.

(1)在图1中,射线BA与ED同向,BC与EF也同向,∠B与∠E的数量关系是: ;
(2)在图2中,射线BA与ED异向,BC与EF也异向,∠B与∠E的数量关系是: ;
(3)在图3中,射线BA与ED同向,BC与EF异向,∠B与∠E有怎样的数量关系,并说明理由;
(4)通过上面(1)、(2)、(3),你可得到的结论是:如果一个角的两边分别平行于另一个角的两边,则这两个角的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有若干个数,第一个数记为a1,第2个数记为a2,第3个数记为a3,……,第n个数记为an,若a1=﹣![]() ,从第二个数起,每一个数都是“1”与它前面那个数的差的倒数.
,从第二个数起,每一个数都是“1”与它前面那个数的差的倒数.
(1)直接写出a2,a3,a4的值;
(2)根据以上结果,计算a1+a2+a3+…+a2017+a2018.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】热气球的探测器显示,从热气球A看一栋楼顶部B的仰角α为45°,看这栋楼底部C的俯角β为60°,热气球与楼的水平距离为100m,求这栋楼的高度(结果保留根号).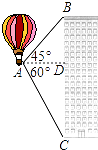
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述
①单项式-![]() 的系数是-
的系数是-![]() ,次数是3次;
,次数是3次;
②用一个平面去截一个圆锥,截面的形状可能是一个三角形;
③在数轴上,点A、B分别表示有理数a、b,若a>b,则A到原点的距离比B到原点的距离大;
④从八边形的一个顶点出发,最多可以画五条对角线;
⑤六棱柱有八个面,18条棱.
其中正确的有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,求AP的长.
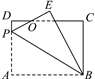
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com