
【题目】直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线y=![]() (x<0)交于点A(﹣1,n).
(x<0)交于点A(﹣1,n).
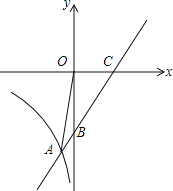
(1)求直线与双曲线的解析式.
(2)连接OA,求∠OAB的正弦值.
【答案】(1)直线与双曲线的解析式分别为y=x﹣4,y=![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据待定系数法,可得直线解析式,根据自变量与函数值的对应关系,可得A点坐标,再根据待定系数法,可得答案;
(2)根据等腰直角三角形的判定,可得△OCB是等腰直角三角形,根据正弦函数,可得OM的长,根据勾股定理,可得OA的长,再根据锐角三角函数的定义,可得答案.
解:(1)将C点代入y=x+b中得到b=﹣4,
∴y=x﹣4;
再将A点带入y=x﹣4得到n=﹣5,
∴A(﹣1,﹣5),
∴m=﹣1×(﹣5)=5,
∴y=![]()
∴直线与双曲线的解析式分别为y=x﹣4,y=![]() ;
;
(2)过点O作OM⊥AC于点M,
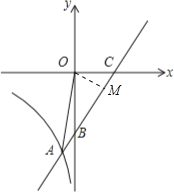
当x=0时,y=﹣4,即B(0,﹣4).
∵OC=OB=4,
∴△OCB是等腰直角三角形,
∴∠OBC=∠OCB=45°
∴在△OMB中 sin45°=![]() ,
,
∴OM=4×![]() =2
=2![]() .
.
∴在直角三角形AOM中,
AO=![]() =
=![]() ,
,
sin∠OAB=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】七、八年级学生分别到雷锋、毛泽东纪念馆参观,共589人,到毛泽东纪念馆的人数是到雷锋纪念馆人数的2倍多56人.设到雷锋纪念馆的人数为人x,可列方程为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛是中国的固有领土,位于中国东海,面积约4400000平方米,数据4400000用科学记数法表示为
A.44×105 B.0.44×105 C.4.4×106 D.4.4×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面证明:
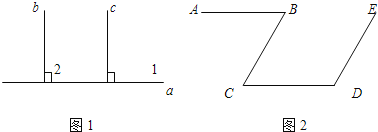
(1)如图1,已知直线b∥c,a⊥c,求证:a⊥b
证明:∵a⊥c ( 已知 )
∴∠1= ( 垂直定义)
∵b∥c (已知 )
∴∠1=∠2 ( )
∴∠2=∠1=90° ( )
∴a⊥b ( )
(2)如图2:AB∥CD,∠B+∠D=180°,求证:CB∥DE
证明:∵AB∥CD (已知 )
∴∠B= ( )
∵∠B+∠D=180° (已知 )
∴∠C+∠D=180° ( )
∴CB∥DE ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30°.
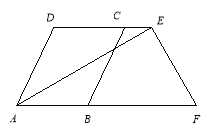
(1)、求证:DC//AB.
(2)、求∠AFE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个边长为3cm的正方形的各边长都增加x cm,则正方形增加的面积y(cm2)与x(cm)之间的函数表达式是( )
A.y=(x+3)2
B.y=x2+6x+6
C.y=x2+6x
D.y=x2
查看答案和解析>>
科目:初中数学 来源: 题型:
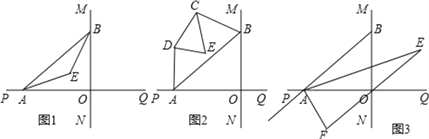
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( )

A.130° B.150° C.160° D.170°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com