
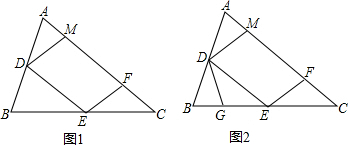
分析 (1)证明∠A=∠DMA,用等角对等边即可证明结论;
(2)由D、E分别是AB、BC的中点,可知DE∥AC,于是∠BDE=∠A,∠DEG=∠C,又∠A=∠AFE,∠AFE=∠C+∠FEC,根据等式性质得∠FEC=∠GDE,根据有两对对应角相等的两三角形相似可证;
(3)通过证明△BDG∽△BED和△EFH∽△ECF,可得BG•BE=EH•EC,又BE=EC,所以EH=BG=5.
解答 (1)证明:如图1所示,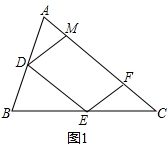 ∵DM∥EF,
∵DM∥EF,
∴∠AMD=∠AFE,
∵∠AFE=∠A,
∴∠AMD=∠A,
∴DM=DA;
(2)证明:如图2所示,
∵D、E分别是AB、BC的中点,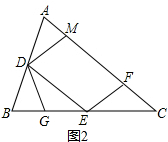 ∴DE∥AC,
∴DE∥AC,
∴∠BDE=∠A,∠DEG=∠C,
∵∠AFE=∠A,
∴∠BDE=∠AFE,
∴∠BDG+∠GDE=∠C+∠FEC,
∵∠BDG=∠C,
∴∠GDE=∠FEC,
∴△DEG∽△ECF;
(3)解:如图3所示,
∵∠BDG=∠C=∠DEB,∠B=∠B,
∴△BDG∽△BED,
∴$\frac{BD}{BE}$=$\frac{BG}{BD}$,
∴BD2=BG•BE,
∵∠AFE=∠A,∠CFH=∠B,
∴∠C=180°-∠A-∠B=180°-∠AFE-∠CFH=∠EFH,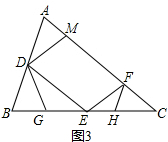
又∵∠FEH=∠CEF,
∴△EFH∽△ECF,
∴$\frac{EH}{EF}$=$\frac{EF}{EC}$,
∴EF2=EH•EC,
∵DE∥AC,DM∥EF,
∴四边形DEFM是平行四边形,
∴EF=DM=DA=BD,
∴BG•BE=EH•EC,
∵BE=EC,
∴EH=BG=5.
点评 本题主要考查了等腰三角形的性质与判定,三角形中位线的性质,平行线的性质,平行四边形的判定与性质以及三角形相似的判定与性质,第三小题是难点,运用两对三角形相似得到比例中项问题,发现等线段是解决问题的关键.


科目:初中数学 来源: 题型:解答题
| 年级 | 七年级 | 八年级 | 九年级 | 高一 | 高二 | 高三 | 合计 |
| 人数/名 | 560 | 520 | 500 | 500 | 480 | 440 | 3000 |
| 调查数/名 | 56 | 52 | 50 | 50 | 48 | 44 | 300 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
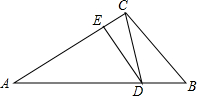 如图,△ABC中,AB=m,BC=n(m、n为常数,n<m).点D是AB上的一点,且∠DCB=∠A,过点D作DE∥BC于点E.
如图,△ABC中,AB=m,BC=n(m、n为常数,n<m).点D是AB上的一点,且∠DCB=∠A,过点D作DE∥BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
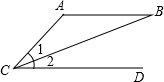 如图,有以下3个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这3个条件中任选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是1.
如图,有以下3个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这3个条件中任选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com