
【题目】如图所示,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD. 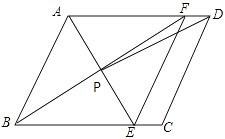
(1)求证:四边形ABEF是菱形.
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
【答案】
(1)解:证明∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAE=∠AEB.
∵AE是角平分线,
∴∠DAE=∠BAE.
∴∠BAE=∠AEB.
∴AB=BE.
同理AB=AF.
∴AF=BE.
∴四边形ABEF是平行四边形.
∵AB=BE,
∴四边形ABEF是菱形.
(2)解:作OH⊥AD于H,如图所示

∵四边形ABEF是菱形,∠ABC=60°,AB=4,
∴AB=AF=4,AP⊥BF,
∴∠ABF=∠AFB=30°,
∴AP= ![]() AB=2,
AB=2,
∴PH= ![]() ,AH=1,DH=AD-AH=5,
,AH=1,DH=AD-AH=5,
∴tan∠ADP= ![]() =
= ![]() .
.
【解析】(1)由平行四边形的性质和角平分线的定义得∠BAE=∠AEB.证出AB=BE.同理AB=AF.得出AF=BE.证出四边形ABEF是平行四边形即可得出结论.(2)作OH⊥AD于H,由菱形的性质得出AB=AF=4,∠ABC=60°,AO⊥BF,∠ABF=∠AFB=30°,由含30°角的直角三角形的性质得出AO= ![]() AB=2,求出OH、DH,即可得出结果。
AB=2,求出OH、DH,即可得出结果。
【考点精析】本题主要考查了平行四边形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.


科目:初中数学 来源: 题型:
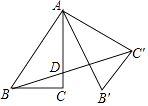
【题目】如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转60° , 点B、C分别落在点B'、C'处,联结BC'与AC边交于点D,那么 ![]() = .
= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax+bx+c上部分点的横坐标x,纵坐标y的对应值如下表,从下表可知:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
下列说法错误的是( )。
A.抛物线与x轴的另一个交点为(3,0);
B.函数的最大值为6;
C.抛物线的对称轴是直线x=0.5;
D.在对称轴的左侧,y随x的增大而增大。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD内接于点O,点E是 ![]() 上的一动点(不与A、B重合),点F是
上的一动点(不与A、B重合),点F是 ![]() 上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论,其中正确的个数是( ). ①
上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论,其中正确的个数是( ). ① ![]() =
= ![]() ; ②△OGH是等腰三角形; ③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为4+
; ②△OGH是等腰三角形; ③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为4+ ![]() .
.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5米,A、B、C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=15米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得EG=3米,小明身高1.6米,则凉亭的高度AB约为( ) 
A.8.5米
B.9米
C.9.5米
D.10米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东64°方向,距离灯塔120海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,求BP和BA的长(结果取整数).
参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05, ![]() 取1.414.
取1.414.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,点E在边BC上,AE=BE,点M是AE的中点,联结CM,点G在线段CM上,作∠GDN=∠AEB交边BC于N. 
(1)如图2,当点G和点M重合时,求证:四边形DMEN是菱形;
(2)如图1,当点G和点M、C不重合时,求证:DG=DN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com