
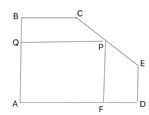
【题目】如图,现有一块钢板余料![]() ,它是矩形缺了一角,
,它是矩形缺了一角,![]()
![]() .王师傅准备从这块余料中裁出一个矩形
.王师傅准备从这块余料中裁出一个矩形![]() (
(![]() 为线段
为线段![]() 上一动点).设
上一动点).设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() .
.
(1)求![]() 与
与![]() 之间的函数关系式,并注明
之间的函数关系式,并注明![]() 的取值范围;
的取值范围;
(2)![]() 为何值时,
为何值时,![]() 取最大值?最大值是多少?
取最大值?最大值是多少?
科目:初中数学 来源: 题型:
【题目】某船自西向东航行,在![]() 处测得某岛
处测得某岛![]() 在北偏东
在北偏东![]() 的方向上,前进
的方向上,前进![]() 海里后到达
海里后到达![]() ,此时,测得海岛
,此时,测得海岛![]() 在北偏东
在北偏东![]() 的方向上,要使船与海岛
的方向上,要使船与海岛![]() 最近,则船应继续向东前进________海里.
最近,则船应继续向东前进________海里.
查看答案和解析>>
科目:初中数学 来源: 题型:
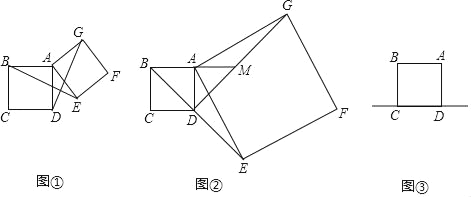
【题目】已知正方形ABCD的边长为2,作正方形AEFG(A,E,F,G四个顶点按逆时针方向排列),连接BE、GD,
(1)如图①,当点E在正方形ABCD外时,线段BE与线段DG有何关系?直接写出结论;
(2)如图②,当点E在线段BD的延长线上,射线BA与线段DG交于点M,且DG=2DM时,求边AG的长;
(3)如图③,当点E在正方形ABCD的边CD所在的直线上,直线AB与直线DG交于点M,且DG=4DM时,直接写出边AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上的一动点(不与A、B重合),CD⊥AB于D,∠OCD的平分线交⊙O于P,则当C在⊙O上运动时,点P的位置( )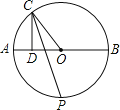
A. 随点C的运动而变化
B. 不变
C. 在使PA=OA的劣弧上
D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
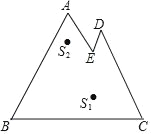
【题目】对于封闭的平面图形,如果图形上或图形内的点S到图形上的任意一点P之间的线段都在图形内或图形上,那么这样的点S称为“亮点”.如图,对于封闭图形ABCDE,S1是“亮点”,S2不是“亮点”,如果AB∥DE,AE∥DC,AB=2,AE=1,∠B=∠C=60°,那么该图形中所有“亮点”组成的图形的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线 AC⊥BD,垂足为O,点E、F、G、H分别为边AD、AB、BC、CD的中点.若AC=10,BD=6,则四边形EFGH的面积为( )
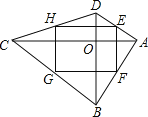
A. 20B. 15C. 30D. 60
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:⑴⑵的计算结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24,
≈2.24,![]() ≈2.45)
≈2.45)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知已知抛物线经过原点O和x轴上一点A(4,0),抛物线顶点为E,它的对称轴与x轴交于点D,直线y=﹣2x﹣1经过抛物线上一点B(﹣2,m)且与y轴交于点C,与抛物线的对称轴交于点F.
(1)求m的值及该抛物线的解析式
(2)P(x,y)是抛物线上的一点,若S△ADP=S△ADC,求出所有符合条件的点P的坐标.
(3)点Q是平面内任意一点,点M从点F出发,沿对称轴向上以每秒1个单位长度的速度匀速运动,设点M的运动时间为t秒,是否能使以Q、A、E、M四点为顶点的四边形是菱形?若能,请直接写出点M的运动时间t的值;若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com