
【题目】(本题满分8分)如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:⑴⑵的计算结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24,
≈2.24,![]() ≈2.45)
≈2.45)

【答案】
(1)AC=2AD=![]() ≈
≈![]()
(2)货物MNQP应挪走,理由略。
【解析】
(本题满分8分)
(1)如图,作AD⊥BC于点D ……………………………………1分

Rt△ABD中,
AD=ABsin45°=4![]() ……2分
……2分
在Rt△ACD中,∵∠ACD=30°
∴AC=2AD=![]() ≈
≈![]() ………………………3分
………………………3分
即新传送带AC的长度约为![]() 米. ………………………………………4分
米. ………………………………………4分
(2)结论:货物MNQP应挪走. ……………………………………5分
解:在Rt△ABD中,BD=ABcos45°=4![]() ……………………6分
……………………6分
在Rt△ACD中,CD=AC cos30°=![]()
∴CB=CD—BD=![]() ≈2.1
≈2.1
∵PC=PB—CB ≈4—2.1=1.9<2 ………………………………7分
∴货物MNQP应挪走. …………………………………………………………8分


科目:初中数学 来源: 题型:
【题目】今年受猪瘟影响,从年初开始,猪肉价格不断走高.消费者王阿姨发现,9月20日当天猪肉的价格是年初的1.5倍;9月20日当天,王阿姨购买4千克猪肉比年初多花了48元.
(1)那么9月20日当天猪肉的价格为每千克多少元?
(2)9月20日,按照(1)中的猪肉价格,某售卖点共卖出1000千克猪肉.9月21日,政府决定投入储备猪肉并规定其销售价在9月20日的基础上下调![]() 出售.该焦卖点按规定价出售一批储备猪肉和非储备猪肉,该售卖点的非储备猪肉仍按9月20日的价格出售,9月21日当天的两种猪肉总销量比9月20日增加了20%,且储备猪肉的销量占总销量的
出售.该焦卖点按规定价出售一批储备猪肉和非储备猪肉,该售卖点的非储备猪肉仍按9月20日的价格出售,9月21日当天的两种猪肉总销量比9月20日增加了20%,且储备猪肉的销量占总销量的![]() ,两种猪肉销售的总金额比9月20日至少提高了
,两种猪肉销售的总金额比9月20日至少提高了![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 有一个角等于![]() 的两个等腰三角形相似
的两个等腰三角形相似
B. 有一个角等于![]() 的两个等腰三角形相似
的两个等腰三角形相似
C. 有一个角等于![]() 的两个等腰三角形相似
的两个等腰三角形相似
D. 有一个角等于![]() 的两个等腰三角形相似
的两个等腰三角形相似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC,



(1)求C点的坐标;
(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OPDE的值;
(3)如图3,已知点F坐标为(2,2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,以下两个结论:①mn为定值;②m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进A,B两种钢笔,若购进A种钢笔2支,B种钢笔3支,共需90元;购进A种钢笔3支,B种钢笔5支,共需145元.
(1)求A、B两种钢笔每支各多少元?
(2)若该文具店要购进A,B两种钢笔共90支,总费用不超过1588元,并且A种钢笔的数量少于B种钢笔的数量,那么该文具店有哪几种购买方案?
(3)文具店以每支30元的价格销售B种钢笔,很快销售一空,于是,文具店决定在进价不变的基础上再购进一批B种钢笔,涨价卖出,经统计,B种钢笔售价为30元时,每月可卖68支;每涨价1元,每月将少卖4支,设文具店将新购进的B种钢笔每支涨价a元(a为正整数),销售这批钢笔每月获利W元,试求W与a之间的函数关系式,并且求出B种铅笔销售单价定为多少元时,每月获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+m与y2=kx+n相交于点A,若点A的横坐标为2,则下列结论中错误的是( )
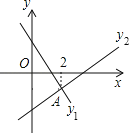
A.k>0B.m>n
C.当x<2时,y2>y1D.2k+n=m﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块全等的含![]() 角的直角三角板按图
角的直角三角板按图![]() 的方式放置,已知
的方式放置,已知![]() ,
,![]() .
.
![]() 固定三角板
固定三角板![]() ,然后将三角板
,然后将三角板![]() 绕点
绕点![]() 顺时针方向旋转至图
顺时针方向旋转至图![]() 所示的位置,
所示的位置,![]() 与
与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
①填空:当旋转角等于![]() 时,
时,![]() ________度;
________度;
②当旋转角等于多少度时,![]() 与
与![]() 垂直?请说明理由.
垂直?请说明理由.
![]() 将图
将图![]() 中的三角板
中的三角板![]() 绕点
绕点![]() 顺时针方向旋转至图
顺时针方向旋转至图![]() 所示的位置,使
所示的位置,使![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,试说明
,试说明![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
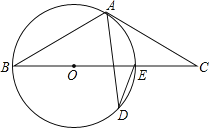
【题目】如图,BE是O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点.
(1)若∠ADE=25°,求∠C的度数;
(2)若AB=AC,CE=2,求⊙O半径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com