练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在四边形ABCD中，对角线 AC⊥BD，垂足为O，点E、F、G、H分别为边AD、AB、BC、CD的中点．若AC=10，BD=6，则四边形EFGH的面积为（　　）

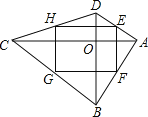
    A. 20B. 15C. 30D. 60

    【答案】B

    【解析】

    有一个角是直角的平行四边形是矩形．利用中位线定理可得出四边形EFGH是矩形，根据矩形的面积公式解答即可．

    ∵点E、F分别为四边形ABCD的边AD、AB的中点，

    ∴EF∥BD，且EF=BD=3．

    同理求得EH∥AC∥GF，且EH=GF=AC=5，

    又∵AC⊥BD，

    ∴EF∥GH，FG∥HE且EF⊥FG．

    四边形EFGH是矩形．

    ∴四边形EFGH的面积=EFEH=3×5=15，即四边形EFGH的面积是15．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某商场为方便顾客使用购物车，准备将滚动电梯的坡面坡度由1：1.8改为1：2.4（如图）．如果改动后电梯的坡面长为13米，求改动后电梯水平宽度增加部分BC的长．

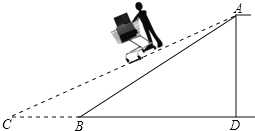
    查看答案和解析>>

    科目：初中数学 来源： 题型：

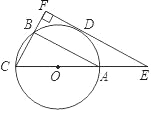
    【题目】如图，△ABC内接于⊙O，AC是⊙O直径，D是的中点，过点D作CB的垂线，分别交CB、CA延长线于点F、E．

    (1)判断直线EF与⊙O的位置关系，并说明理由；

    (2)若sinE＝，求AB：EF的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

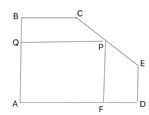
    【题目】如图，现有一块钢板余料，它是矩形缺了一角， .王师傅准备从这块余料中裁出一个矩形（为线段上一动点）.设，矩形的面积为.

    （1）求与之间的函数关系式，并注明的取值范围；

    （2）为何值时，取最大值？最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

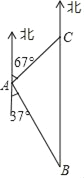
    【题目】如图，在港口A的南偏东37°方向的海面上，有一巡逻艇B，A、B相距20海里，这时在巡逻艇的正北方向及港口A的北偏东67°方向上，有一渔船C发生故障．得知这一情况后，巡逻艇以25海里/小时的速度前往救援，问巡逻艇能否在1小时内到达渔船C处？

    （参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，sin67°≈，cos67°≈，tan67°≈）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校环保志愿者协会对该市城区的空气质量进行调查，从全年365天中随机抽取了80天的空气质量指数（AQI）数据，绘制出三幅不完整的统计图表，请根据图表中提供的信息解答下列问题：

    AQI指数

    质量等级

    天数（天）

    0-50

    优

    m

    51-100

    良

    44

    101-150

    轻度污染

    n

    151-200

    中度污染

    4

    201-300

    重度污染

    2

    300以上

    严重污染

    2

    （1）统计表中m= ，n= ，扇形统计图中，空气质量等级为“良”的天数占 %；

    （2）补全条形统计图，并通过计算估计该市城区全年空气质量等级为“优”和“良”的天数共多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知点A、B的坐标分别为（8，0）、（0，2），C是AB的中点，过点C作y轴的垂线，垂足为D，动点P从点D出发，沿DC向点C匀速运动，过点P作x轴的垂线，垂足为E，连接BP、EC．当BP所在直线与EC所在直线垂直时，点P的坐标为____

    查看答案和解析>>

    科目：初中数学 来源： 题型：

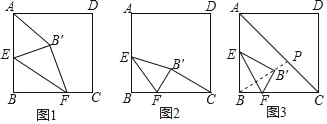
    【题目】正方形ABCD的边长是10，点E是AB的中点，动点F在边BC上，且不与点B、C重合，将△EBF沿EF折叠，得到△EB′F．

    （1）如图1，连接AB′．

    ①若△AEB′为等边三角形，则∠BEF等于多少度．

    ②在运动过程中，线段AB′与EF有何位置关系？请证明你的结论．

    （2）如图2，连接CB′，求△CB′F周长的最小值．

    （3）如图3，连接并延长BB′，交AC于点P，当BB′＝6时，求PB′的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

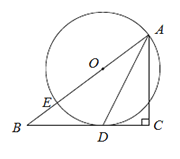
    【题目】已知：如图，在Rt△ABC中，∠C=90°，点E在斜边AB上，以AE为直径的⊙O与BC边相切于点D，连结AD.

    （1）求证：AD是∠BAC的平分线；

    （2）若AC=3，BC=4，求⊙O的半径.

    查看答案和解析>>

    同步练习册答案