
����Ŀ������ѧϰ�����Ķ����н�����̣�
��һԪ���β���ʽ��x2��5x��0��
�⣺��x2��5x=0����ã�x1=0��x2=5����������y=x2��5x��x��Ľ�������Ϊ��0��0���ͣ�5��0�����������κ���y=x2��5x�Ĵ���ͼ����ͼ��ʾ������ͼ���֪����x��0����x��5ʱ����ͼ��λ��x���Ϸ�����ʱy��0����x2��5x��0�����ԣ�һԪ���β���ʽx2��5x��0�Ľ⼯Ϊ��x��0��x��5��
ͨ��������������̵�ѧϰ����������˼·�ͷ�������������⣺
��1��������������У�����������ѧ˼���е��� �� ��ֻ����ţ�
��ת��˼�� �ڷ�������˼�� �����ν��˼��
��2��һԪ���β���ʽx2��5x��0�Ľ⼯Ϊ ��
��3�������Ƶķ���д��һԪ���β���ʽ�Ľ⼯��x2��2x��3��0�� ��
���𰸡�
��1���٣���
��2��0��x��5
��3��x����1��x��3
���������⣺��1��������������У�����������ѧ˼���еĢٺۣ͢�
���Դ��ǣ��٣��ۣ���2����ͼ���֪����0��x��5ʱ����ͼ��λ��x���·���
��ʱy��0����x2��5x��0��
��һԪ���β���ʽx2��5x��0�Ľ⼯Ϊ��0��x��5��
���Դ��ǣ�0��x��5����3����x2��2x��3=0��
��ã�x1=3��x2=��1��
��������y=x2��2x��3��x��Ľ�������Ϊ��3��0���ͣ���1��0����
�������κ���y=x2��2x��3�Ĵ���ͼ����ͼ��ʾ����
��ͼ���֪����x����1����x��3ʱ����ͼ��λ��x���Ϸ���
��ʱy��0����x2��2x��3��0��
��һԪ���β���ʽx2��2x��3��0�Ľ⼯Ϊ��x����1��x��3��
���Դ���x����1��x��3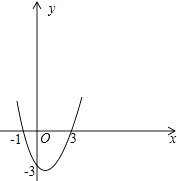
�����㾫����������������������Ľ������Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪һԪ���η��̵Ľ������Ӧ�Ķ��κ�����ͼ����x��Ľ������꣮���һԪ���η����е�b2-4ac���ڶ��κ����б�ʾͼ����x���Ƿ��н��㣮��b2-4ac>0ʱ��ͼ����x�����������㣻��b2-4ac=0ʱ��ͼ����x����һ�����㣻��b2-4ac<0ʱ��ͼ����x��û�н��㣮


 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DF��AB������ΪF��DE��DG����ADG�͡�AED������ֱ�Ϊ40��28�����EDF�����Ϊ��������

A. 12 B. 6 C. 7 D. 8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����MΪֱ��AB��һ���㣬 ![]() ���ǵȱ������Σ�����BN
���ǵȱ������Σ�����BN
![]() ��֤��
��֤�� ![]() ��
��
![]() �ֱ�д����M����ͼ2��ͼ3��ʾλ��ʱ���߶�AB��BM��BN����֮���������ϵ
�ֱ�д����M����ͼ2��ͼ3��ʾλ��ʱ���߶�AB��BM��BN����֮���������ϵ![]() ����֤��
����֤��![]() ��
��
![]() ��ͼ4����
��ͼ4����![]() ʱ��֤����
ʱ��֤���� ![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȱ�������ABC�У���E��AB�ϣ���D��CB���ӳ����ϣ���ED=EC����ͼ����ȷ���߶�AE��DB�Ĵ�С��ϵ����˵����������
��1������EΪAB���е�ʱ����ͼ1��ȷ���߶�AE��DB�Ĵ�С��ϵ��ֱ��д�����ۣ�AE�� ��DB
����������������������=������
��2��֤����ó������ϣ�1������ͼ2������E��EF��BC����AC�ڵ�F��

��3���ڵȱ�������ABC�У���E��ֱ��AB�ϣ���D��ֱ��BC�ϣ���ED = EC������ABC�ı߳�Ϊ1��AE = 2����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AD�ǡ�BAC��ƽ���ߣ�E��F�ֱ�ΪAB��AC�ϵĵ㣬�ҡ�EDF+��EAF=180������֤DE=DF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ȱ���ABC�ĸ�Ϊ6����������������ڵ�ƽ������һ��P������P��ֱ��AB�ľ�����1����P��ֱ��AC�ľ�����3�����P��ֱ��BC�ľ��������_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+bx+c��x���ڵ�A����3��0���͵�B����y���ڵ�C��0��3����
��1���������ߵĺ�������ʽ��
��2������P���������ϣ���S��AOP=4SBOC �� ���P�����ꣻ
��3����ͼb�����Q���߶�AC�ϵ�һ���㣬��DQ��x�ᣬ���������ڵ�D�����߶�DQ���ȵ����ֵ��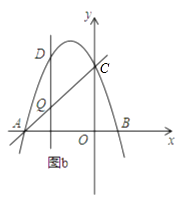
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У����ڵ�
�У����ڵ�![]() �����ǰѵ�
�����ǰѵ�![]() ������
������![]() �������㣮��֪��
�������㣮��֪��![]() ��������Ϊ
��������Ϊ![]() ����
����![]() ��������Ϊ
��������Ϊ![]() ����
����![]() ��������Ϊ
��������Ϊ![]() �������εõ���
�������εõ���![]() ����
����![]() ������Ϊ
������Ϊ![]() ������
������![]() �ڵ������ޣ���
�ڵ������ޣ���![]() ��Χ�ֱ�Ϊ______________.
��Χ�ֱ�Ϊ______________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ABC�У���ABC=60�㣬BC=2cm��BDƽ����ABC��AC�ڵ�D����M��N�ֱ���BD��BC���ϵĶ��㣬��MN+MC����Сֵ��_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com