
【题目】在锐角△ABC中,∠ABC=60°,BC=2cm,BD平分∠ABC交AC于点D,点M,N分别是BD和BC边上的动点,则MN+MC的最小值是_____.

【答案】![]() .
.
【解析】
如图,在BA上截取BE=BN,连接CE,证明△BME≌△BMN,根据全等三角形的性质可得ME=MN.所以CM+MN=CM+ME≥CE,由此可得CM+MN有最小值.当CE是点C到直线AB的距离时,CE有最小,根据已知条件求得CE的长,由此即可求解.
如图,在BA上截取BE=BN,连接CE.
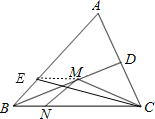
∵∠ABC的平分线交AC于点D,
∴∠EBM=∠NBM,
在△BME与△BMN中,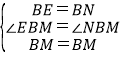 ,
,
∴△BME≌△BMN,
∴ME=MN.
∴CM+MN=CM+ME≥CE.
∴CM+MN有最小值.
当CE是点C到直线AB的距离时,CE最小,
∵∠ABC=60°,BC=2cm,
∴当CE⊥AB时,可得CE=![]() ,
,
∴CM+MN的最小值是![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:x2﹣5x>0.
解:设x2﹣5x=0,解得:x1=0,x2=5,则抛物线y=x2﹣5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2﹣5x的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即x2﹣5x>0,所以,一元二次不等式x2﹣5x>0的解集为:x<0或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的和 . (只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式x2﹣5x<0的解集为 .
(3)用类似的方法写出一元二次不等式的解集:x2﹣2x﹣3>0. .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A(2,0),B(0,2),点P是抛物线上一动点,连接BP,OP. 
(1)求这条抛物线的解析式;
(2)若△BOP是以BO为底边的等腰三角形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E分别为AB、AC上的点,∠BDE、∠CED的平分线分别交BC于点F、G,EG∥AB.若∠BGE=110°,则∠BDF的度数为___________
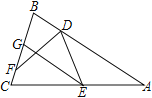
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表:
x | … | ﹣3 | - | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中m= .
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分; 
(3)观察函数图象,写出2条函数的性质;
(4)进一步探究函数图象发现:
①函数图象与x轴有个交点,所对应的方程x2﹣2|x|=0有个实数根;
②方程x2﹣2|x|=2有个实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com