
如图,在矩形ABCD中,AB=2BC,E为CD上一点,且AE=AB,M为AE的中点.下列结论:
①DM=DA;②EB平分∠AEC;③S△ABE=S△ADE;④BE2=2AE•EC.其中结论正确的个数是( )


A.1 B.2 C.3 D.4
C【考点】相似三角形的判定与性质;勾股定理;矩形的性质.
【分析】①由于DM是直角△ADE斜边AE上的中线,欲证DM=DA,只需证明AD=
 AE即可;②在直角△ADE中,由于∠ADE=90°,AD=
AE即可;②在直角△ADE中,由于∠ADE=90°,AD=
 AE,得出∠DEA=30°,然后分别算出∠AEB与∠CEB的度数即可;③由于S△ABE=
AE,得出∠DEA=30°,然后分别算出∠AEB与∠CEB的度数即可;③由于S△ABE=
 S矩形ABCD,S△ADE<
S矩形ABCD,S△ADE<
 S矩形ABCD,从而进行判断;④如果设BC=DA=a,则可用含a的代数式表示BC、AE、EC的长度,然后在直角△BCE中运用勾股定理算出BE2的值,再算出2AE•EC的值,比较即可.
S矩形ABCD,从而进行判断;④如果设BC=DA=a,则可用含a的代数式表示BC、AE、EC的长度,然后在直角△BCE中运用勾股定理算出BE2的值,再算出2AE•EC的值,比较即可.
【解答】解:①∵在直角△ADE中,∠ADE=90°,M为AE的中点,∴DM=
 AE,∵AE=AB,AB=2BC=2DA,∴DM=DA,正确;
AE,∵AE=AB,AB=2BC=2DA,∴DM=DA,正确;
②在直角△ADE中,∠ADE=90°,AD=
 AE,∴∠DEA=30°.∵CD∥AB,∴∠EAB=∠DEA=30°,∠CEB=∠ABE.在△EAB中,∠EAB=30°,AE=AB,∴∠AEB=∠ABE=75°,∴∠CEB=75°,∴EB平分∠AEC,正确;
AE,∴∠DEA=30°.∵CD∥AB,∴∠EAB=∠DEA=30°,∠CEB=∠ABE.在△EAB中,∠EAB=30°,AE=AB,∴∠AEB=∠ABE=75°,∴∠CEB=75°,∴EB平分∠AEC,正确;
③∵S△ABE=
 S矩形ABCD,S△ADE<S△ADC=
S矩形ABCD,S△ADE<S△ADC=
 S矩形ABCD,∴S△ABE>S△ADE,错误;
S矩形ABCD,∴S△ABE>S△ADE,错误;
④在矩形ABCD中,设BC=DA=a,则AE=AB=DC=2BC=2a,DE=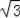
 AD=
AD=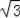
 a,∴EC=(2﹣
a,∴EC=(2﹣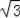
 )a.在直角△BCE中,BE2=BC2+CE2=a2+[(2﹣
)a.在直角△BCE中,BE2=BC2+CE2=a2+[(2﹣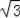
 )a]2=(8﹣4
)a]2=(8﹣4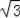
 )a2,2AE•EC=2×2a×(2﹣
)a2,2AE•EC=2×2a×(2﹣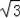
 )a=(8﹣4
)a=(8﹣4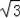
 )a2,正确.
)a2,正确.
故选C.
【点评】本题主要考查了直角三角形、矩形的性质以及多边形的面积,勾股定理.综合性较强,有一定难度.


科目:初中数学 来源: 题型:
如图,已知抛物线y=ax2+bx﹣3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为
 .设⊙M与y轴交于D,抛物线的顶点为E.
.设⊙M与y轴交于D,抛物线的顶点为E.
(1)求m的值及抛物线的解析式;
(2)设∠DBC=α,∠CBE=β,求sin(α﹣β)的值;
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示 ,点G在线段D
,点G在线段D K上,正方形BEFG的边长为4,则△DEK的面积为( )
K上,正方形BEFG的边长为4,则△DEK的面积为( )
A.10 B.12 C.14 D.16

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com