
分析 如图1,当点P在CD上时,由折叠的性质得到四边形PFBE是正方形,EF过点C,根据勾股定理即可得到结果;如图2当点P在AD上时,过E作EQ⊥AB于Q,根据勾股定理得到PB=$\sqrt{A{P}^{2}+A{B}^{2}}$=$\sqrt{{3}^{2}{+9}^{2}}$=3$\sqrt{10}$,推出△ABP∽△EFQ,列比例式即可得到结果.
解答 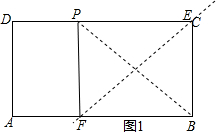 解:如图1,当点P在CD上时,
解:如图1,当点P在CD上时,
∵PD=3,CD=AB=9,
∴CP=6,∵EF垂直平分PB,
∴四边形PFBE是正方形,EF过点C,
∴EF=6$\sqrt{2}$,
如图2,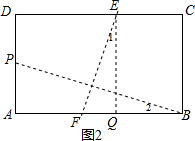 当点P在AD上时,
当点P在AD上时,
过E作EQ⊥AB于Q,
∵PD=3,AD=6,
∴AP=3,
∴PB=$\sqrt{A{P}^{2}+A{B}^{2}}$=$\sqrt{{3}^{2}{+9}^{2}}$=3$\sqrt{10}$,
∵EF垂直平分PB,
∴∠1=∠2,
∵∠A=∠EQF,
∴△ABP∽△EFQ,
∴$\frac{EF}{PB}=\frac{EQ}{AB}$,
∴$\frac{EF}{3\sqrt{10}}=\frac{6}{9}$,
∴EF=2$\sqrt{10}$,
综上所述:EF长为6$\sqrt{2}$或2$\sqrt{10}$.
故答案为:6$\sqrt{2}$或2$\sqrt{10}$.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:选择题
| A. | 3a+4b=12a | B. | (ab3)2=ab6 | ||
| C. | (5a2-ab)-(4a2+2ab)=a2-3ab | D. | x12÷x6=x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
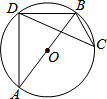 如图,△ABD的三个顶点在⊙O上,AB是直径,点C在⊙O上,且∠ABD=52°,则∠BCD等于( )
如图,△ABD的三个顶点在⊙O上,AB是直径,点C在⊙O上,且∠ABD=52°,则∠BCD等于( )| A. | 32° | B. | 38° | C. | 52° | D. | 66° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地.甲乙两车距A地的路程y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.
甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地.甲乙两车距A地的路程y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 147 | B. | 151 | C. | 152 | D. | 156 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com