【题目】如图,圆柱形容器中，高为120cm，底面周长为100cm，在容器内壁离容器底部40cm，的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿40cm与蚊子相对的点A处，
则壁虎捕捉蚊子的最短距离为Cm（容器厚庋忽略不计）.
【答案】130
【解析】解：如图,将容器侧面展开,作A关于EC的对称点A′,连接A′B交EC于F,则A′B即为最短距离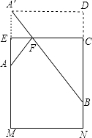 
∵高为120cm，底面周长为100cm，在容器内壁离容器底部40cm的点B处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿40cm与蚊子相对的点A处，
∴A′D=50cm，BD=120cm，
∴在直角△A′DB中,A′B=
=
=130cm .
所以答案是：130 。
【考点精析】利用几何体的展开图和轴对称-最短路线问题对题目进行判断即可得到答案，需要熟知沿多面体的棱将多面体剪开成平面图形，若干个平面图形也可以围成一个多面体；同一个多面体沿不同的棱剪开，得到的平面展开图是不一样的，就是说：同一个立体图形可以有多种不同的展开图；已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．
科目：初中数学 来源： 题型：
【题目】如图1，点
、
、
、
分别在矩形
的边
、
、
、
上，
.
求证：
.(
表示面积)
实验探究：
某数学实验小组发现：若图1中
，点
在
上移动时，上述结论会发生变化，分别过点
、
作
边的平行线，再分别过点
、
作
边的平行线，四条平行线分别相交于点
、
、
、
，得到矩形
.
如图2，当
时，若将点
向点
靠近(
)，经过探索，发现：
.
如图3，当
时，若将点
向点
靠近(
，请探索
、
与
之间的数量关系，并说明理由.
迁移应用：
请直接应用“实验探究”中发现的结论解答下列问题.
(1)如图4，点
、
、
、
分别是面积为25的正方形
各边上的点，已知
，
，
，
，求
的长.
(2)如图5，在矩形
中，
，
，点
、
分别在边
、
上，
，
，点
、
分别是边
、
上的动点，且
，连接
、
，请直接写出四边形
面积的最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点A（m+1，–2）和点B（3，n–1），若直线AB∥x轴，且AB=4，则m+n的值为（ ）
A. –3B. 5
C. 7或–5D. 5或–3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
