
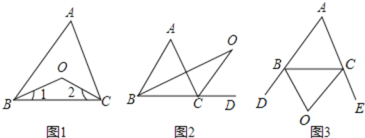
【题目】认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
(1)如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,试证明∠BOC=90°+![]()
(2)如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
(3)如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
【答案】(1)见解析;(2)∠BOC=![]() ,理由见解析;(3)∠BOC=90°-
,理由见解析;(3)∠BOC=90°-![]()
【解析】
(1)利用△ABC和△BOC的内角和为180°进行角度转化可得结论;
(2)设∠ABO=x,∠ACO=y,利用△ABC和△OBC的内角和,可得出2个关于x、y、∠A、∠BOC的方程,消去x、y可得;
(3)设∠DBO=x,∠ECO=y,利用△ABC和△OBC的内角和,可得出2个关于x、y、∠A、∠BOC的方程,消去x、y可得.
(1)∵OB、OC分别时∠ABC和∠ACB的角平分线
∴∠ABO=2∠1,∠ACB=2∠2
在△ABC中,∠A+2∠1+2∠2=180°,化简得:∠A+2(∠1+∠2)=180°
在△BOC中,∠1+∠2+∠BOC=180°,化简得:∠1+∠2=180°-∠BOC,代入上式得:
∠A+2(180°-∠BOC)=180°
化简得:∠BOC=90°+![]()
(2)设∠ABO=x,∠ACO=y
∵O是∠ABC与外角∠ACD的平分线BO和CO的交点
∴∠OBC=∠OBA=x,∠OCD=∠OCA=y,∠ACB=180°-2y
∴在△ABC中,∠A+2x+(180°-2y)=180°,化简得:∠A=2(y-x)
在△BOC中,x+∠BOC+(180°-2y+y)=180°,化简得:∠BOC=(y-x)
∴∠BOC=![]()
(3)设∠DBO=x,∠ECO=y
同理,∠OBC=x,∠OCB=y,∠ABC=180°-2x,∠ACB=180°-2y
∴在△ABC中,∠A+(180°-2x)+ (180°-2y)=180°,化简得:2(x+y)-∠A=180°
在△OBC中,x+y+∠BOC=180°,化简得:x+y=180°-∠BOC,代入上式得:
∠A+2∠BOC=180°,即:∠BOC=90°-![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,∠B=70°,∠BCE=20°,∠CEF=130°,请判断AB与EF的位置关系,并说明理由.
解: ,理由如下:
∵AB∥CD,
∴∠B=∠BCD,( )
∵∠B=70°,
∴∠BCD=70°,( )
∵∠BCE=20°,
∴∠ECD=50°,
∵∠CEF=130°,
∴ + =180°,
∴EF∥ ,( )
∴AB∥EF.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区100个家庭收入按从高到低是5800,……,10000元各不相同,在输入计算时,把最大的数错误地输成100000元,则依据错误的数据算出的平均数比实际平均数多( )
A. 900元B. 942元C. 90000元D. 9000元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋内装有四张完全相同的卡片,分别标有数字1、2、3、4。
(1)若任取一张卡片,上面所标数字是不小于3的概率为;
(2)在口袋中任取两张卡片:请你利用树状图或列表法求出这两张卡片上的数字的积为奇数的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线![]() ,点
,点![]() 为平面上一点,连接
为平面上一点,连接![]() 与
与![]() .
.
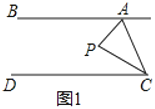
(1)如图1,点![]() 在直线
在直线![]() 、
、![]() 之间,当
之间,当![]() ,
,![]() 时,求
时,求![]() .
.
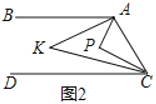
(2)如图2,点![]() 在直线
在直线![]() 、
、![]() 之间
之间![]() 左侧,
左侧,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,写出
,写出![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
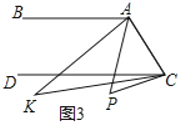
(3)如图3,点![]() 落在
落在![]() 下方,
下方,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,
,![]() 与
与![]() 有何数量关系?并说明理由.
有何数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为( ).
A.3
B.![]()
C.5
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学采用随机的方式对学生掌握安全知识的情况进行测评,并按成绩高低分成优、良、中、差四个等级进行统计,绘制了下面两幅尚不完整的统计图.请根据有关信息解答: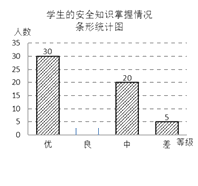

(1)接受测评的学生共有人,扇形统计图中“优”部分所对应扇形的圆心角为°,并补全条形统计图;
(2)若该校共有学生1200人,请估计该校对安全知识达到“良”程度的人数;
(3)测评成绩前五名的学生恰好3个女生和2个男生,现从中随机抽取2人参加市安全知识竞赛,请用树状图或列表法求出抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小慧两位同学在数学活动课中,把长为30cm,宽为10cm的长方形白纸条粘合起来,小明按如图甲所示的方法粘合起来得到长方形ABCD,粘合部分的长度为6cm,小慧按如图乙所示的方法粘合起来得到长方形 A1B1C1D1 ,粘合部分的长度为4cm。若长为30cm,宽为10cm的长方形白纸共有100张,则小明应分配到( )张长方形白纸条,才能使小明和小慧按各自粘合起来的长方形面积相等(要求100张长方形白纸条全部用完)

A.41
B.42
C.43
D.44
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com