
【题目】平面直角坐标系中,横坐标为2的点A在反比例函数y![]() (k>0)的图象上,过点A作AB⊥x轴于点B,
(k>0)的图象上,过点A作AB⊥x轴于点B,![]() .
.
(1)求k的值;
(2)在x轴的负半轴上找点P,将点A绕点P顺时针旋转90°,其对应点A落在此反比例函数第三象限的图象上,求点P的坐标;
(3)直线y![]() x+n(n<0)与AB的延长线交于点C,与反比例函数图象交于点E,若点E到直线AB的距离等于AC,求n的值.
x+n(n<0)与AB的延长线交于点C,与反比例函数图象交于点E,若点E到直线AB的距离等于AC,求n的值.

【答案】(1)k=8;(2)点P坐标为(﹣1![]() ,0);(3)n的值为﹣3或
,0);(3)n的值为﹣3或![]() .
.
【解析】
(1)设OA![]() a,则AB=2a,OB=2,利用勾股定理解出a,得到A点,代入得到k即可;(2)过点A′作AG⊥x轴交于点G,设点P(a,0),易证△PAB≌△A′PG,得到点A′的坐标为(a+4,a﹣2),得(a+4)(a﹣2)=8,解出a即可;(3)设线y
a,则AB=2a,OB=2,利用勾股定理解出a,得到A点,代入得到k即可;(2)过点A′作AG⊥x轴交于点G,设点P(a,0),易证△PAB≌△A′PG,得到点A′的坐标为(a+4,a﹣2),得(a+4)(a﹣2)=8,解出a即可;(3)设线y![]() x+n(n<0)与AB和双曲线分别交于点C、点E(E′),过点E(E′)作E(′E)F(F′)⊥AB交于点F(F′),E点有两种情况,在第一象限或者第三象限,将直线表达式与反比例函数表达式联立,用n表示出EF,E到直线AB的距离为FE等于AC,得到方程解出n即可
x+n(n<0)与AB和双曲线分别交于点C、点E(E′),过点E(E′)作E(′E)F(F′)⊥AB交于点F(F′),E点有两种情况,在第一象限或者第三象限,将直线表达式与反比例函数表达式联立,用n表示出EF,E到直线AB的距离为FE等于AC,得到方程解出n即可
解:(1)![]() ,设:OA
,设:OA![]() a,则AB=2a,OB=2,
a,则AB=2a,OB=2,
由勾股定理得:(![]() a)2=(2a)2+4,解得:a=2,
a)2=(2a)2+4,解得:a=2,
则点A(2,4),
则k=2×4=8;
(2)点A绕点P顺时针旋转90°,点A对应点A′落在此反比例函数第三象限的图象上,
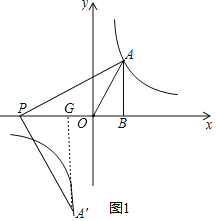
过点A′作AG⊥x轴交于点G,设点P(a,0),
∵∠PAB+∠BPA=90°,∠BPA+∠A′PG=90°,
∴∠A′PG=∠PAB,
∠ABP=∠A′GP=90°,PA=PA′,
∴△PAB≌△A′PG(AAS),
∴PG=AB=4,GA′=PB=2﹣a,
则点A′的坐标为(a+4,a﹣2),
则(a+4)(a﹣2)=8,
解得:a=﹣1![]() (正值已舍去)
(正值已舍去)
故点P坐标为(﹣1![]() ,0);
,0);
(3)设线y![]() x+n(n<0)与AB和双曲线分别交于点C、点E(E′)
x+n(n<0)与AB和双曲线分别交于点C、点E(E′)
过点E(E′)作E(′E)F(F′)⊥AB交于点F(F′),
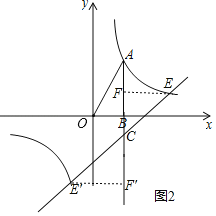
①当直线与双曲线交点为E时,
则点C(2,1+n),AC=4﹣1﹣n=3﹣n,
将直线表达式与反比例函数表达式联立并整理得:x2+2nx﹣16=0,
解得:x=﹣n±![]() ,则xE=﹣n
,则xE=﹣n![]() ,
,
则EF=﹣n![]() 2,
2,
E到直线AB的距离为FE等于AC,
则﹣n![]() 2=3﹣n,
2=3﹣n,
解得:n=﹣3(正值已舍去);
②当直线与双曲线交点为E′时,
同理可得:n![]() ;
;
故:n的值为﹣3或![]() .
.


科目:初中数学 来源: 题型:
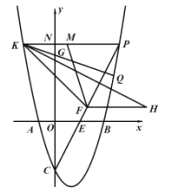
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .
.
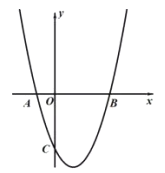
(1)如图,求抛物线的解析式;
(2)如图,点![]() 是第一象限抛物线上的一个动点,连接
是第一象限抛物线上的一个动点,连接![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式(不要求写出自变量
之间的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
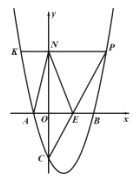
(3)如图,在(2) 的条件下,点![]() 是
是![]() 中点,过点
中点,过点![]() 作
作![]() 的垂线与过点
的垂线与过点![]() 平行于
平行于![]() 轴的直线交于点
轴的直线交于点![]() ,
, ![]() ,点
,点![]() 为第一象限内直线
为第一象限内直线![]() 下方抛物线上一点,连接
下方抛物线上一点,连接![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 上一点,连接
上一点,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,求点
,求点![]() 坐标
坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
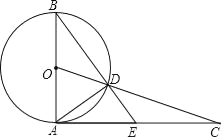
【题目】如图,AB是⊙O的直径,点C为⊙O外一点,连接OC交⊙O于点D,连接BD并延长交线段AC于点E,∠CDE=∠CAD.
(1)求证:CD2=ACEC;
(2)判断AC与⊙O的位置关系,并证明你的结论;
(3)若AE=EC,求tanB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校7年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.

(1)在平面直角坐标系中画出探险路线图;
(2)分别写出A、B、C、D、P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市从2018年1月1日开始,禁止燃油助力车上路,于是电动自行车的市场需求量日渐增多.某商店计划最多投入8万元购进A、B两种型号的电动自行车共30辆,其中每辆B型电动自行车比每辆A型电动自行车多500元.用5万元购进的A型电动自行车与用6万元购进的B型电动自行车数量一样.
(1)求A、B两种型号电动自行车的进货单价;
(2)若A型电动自行车每辆售价为2800元,B型电动自行车每辆售价为3500元,设该商店计划购进A型电动自行车m辆,两种型号的电动自行车全部销售后可获利润y元.写出y与m之间的函数关系式;
(3)在(2)的条件下,该商店如何进货才能获得最大利润?此时最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学考试中,小明有一道选择题(只能在四个选项A、B、C、D中选一个)不会做,便随机选了一个答案;小亮有两道选择题都不会做,他也随机选了两个答案.
(1)小明随机选的这个答案,答对的概率是 ;
(2)通过画树状图或列表法求小亮两题都答对概率是多少?
(3)这个班数学老师参加集体阅卷,在阅卷的过程中,发现学生的错误率较高.他想:若这10道选择题都是靠随机选择答案,则这10道选择题全对的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两动点分别从正方形ABCD的顶点A,C同时沿正方形的边开始移动,甲按顺时针方向环形,乙按逆时针方向环行,若乙的速度是甲的3倍,那么它们第一次相遇在AD边上,请问它们第2015次相遇在( )边上.
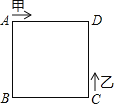
A. ADB. DCC. BCD. AB
查看答案和解析>>
科目:初中数学 来源: 题型:
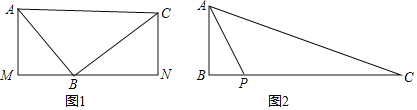
【题目】在△ABC中,∠ABC=90°
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为点M,N,求证:△ABM∽△BCN;
(2)如图2,P是BC边上一点,∠BAP=∠C,tan∠PAC=![]() ,BP=2cm,求CP的长.
,BP=2cm,求CP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com