
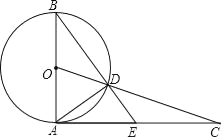
【题目】如图,AB是⊙O的直径,点C为⊙O外一点,连接OC交⊙O于点D,连接BD并延长交线段AC于点E,∠CDE=∠CAD.
(1)求证:CD2=ACEC;
(2)判断AC与⊙O的位置关系,并证明你的结论;
(3)若AE=EC,求tanB的值.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)根据相似三角形的判定证明△CDE∽△CAD,再根据相似三角形的性质定理即可证明;
(2)根据圆周角定理得到∠ADB=90°,再利用等量代换得到∠B=∠CAD,进而得到∠BAC=∠BAD+∠CAD=∠B+∠BAD=90°,即可得证;
(3)根据(1)与题意得到CD=![]() CE,利用相似三角形的性质与等量代换可得tanB=tan∠CAD=
CE,利用相似三角形的性质与等量代换可得tanB=tan∠CAD=![]() .
.
(1)证明:∵∠CDE=∠CAD,∠C=∠C,
∴△CDE∽△CAD,
∴![]() ,
,
∴CD2=CACE;
(2)AC与⊙O相切,
证明:∵AC是⊙O的直径,
∴∠ADB=90°,
∴∠BAD+∠B=90°,
∵OB=OD,
∴∠B=∠ODB,
∵∠ODB=∠CDE,∠CDE=∠CAD,
∴∠B=∠CAD,
∴∠BAC=∠BAD+∠CAD=∠B+∠BAD=90°,
∴BA⊥AC,
∴AC与⊙O相切;
(3)解:∵AE=EC,
∴CD2=CACE=(AE+CE)CE=2CE2,
∴CD=![]() CE,
CE,
∵△CDE∽△CAD,
∴![]() ,
,
∵∠ADE=180°-∠ADB=90°,∠B=∠CAD,
∴tanB=tan∠CAD=![]() .
.


科目:初中数学 来源: 题型:
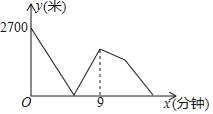
【题目】A,B两地之间有一条直线跑道,甲,乙两人分别从A,B同时出发,相向而行匀速跑步,且乙的速度是甲速度的80%,当甲,乙分别到达B地,A地后立即调头往回跑,甲的速度保持不变,乙的速度提高25%(仍保持匀速前行),甲,乙两人之间的距离y(米)与跑步时间x(分钟)之间的关系如图所示,则他们在第二次相遇时距B地_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像与x轴交于点(-2,0)、(
的图像与x轴交于点(-2,0)、(![]() ),且
),且![]() ,与y轴的正半轴的交点在(0,2)的下方,则下列结论中:①ab>0;②4a-2b+c=0;③2a-b+1<0;④a<b<c,其中正确的结论有( ).
,与y轴的正半轴的交点在(0,2)的下方,则下列结论中:①ab>0;②4a-2b+c=0;③2a-b+1<0;④a<b<c,其中正确的结论有( ).
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校兴趣小组就“最想去的金华最美村落”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的最美乡村![]() 下面是根据调查结果绘制出的不完整的统计图
下面是根据调查结果绘制出的不完整的统计图
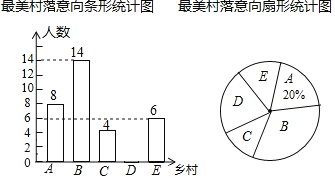
请根据图中提供的信息,解答下列问题:
![]() 被调查的学生总人数为______人;
被调查的学生总人数为______人;
![]() 扇形统计图中“最想去乡村D”的扇形圆心角的度数为______;
扇形统计图中“最想去乡村D”的扇形圆心角的度数为______;
![]() 若该校共有800名学生,请估计“最想去乡村B”的学生人数.
若该校共有800名学生,请估计“最想去乡村B”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有除颜色外其余均相同的红、蓝两种球,已知其中红球有3个,且从中任意摸出一个是红球的概率为0.75.
(1)根据题意,袋中有 个蓝球.
(2)若第一次随机摸出一球,不放回,再随机摸出第二个球.请用画树状图或列表法求“摸到两球中至少一个球为蓝球(记为事件A)”的概率P(A).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
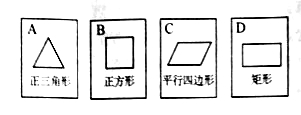
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委计划在元且期间组织优秀团员到敬老院去服务,现选出了10名优秀团员参加服务,其中男生6人,女生4人.
![]() 若从这10人中随机选一人当队长,求选中女生当队长的概率;
若从这10人中随机选一人当队长,求选中女生当队长的概率;
![]() 现决定从甲、乙中选一人当队长,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则选甲为队长;否则,选乙为队长
现决定从甲、乙中选一人当队长,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则选甲为队长;否则,选乙为队长![]() 试问这个游戏公平吗?请用树状图或列表法说明理由.
试问这个游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22017
首先设S=1+2+22+23+24+…+22017 ① 则2S=2+22+23+24+25+…+22018 ②
②﹣①得S=22018﹣1 即1+2+22+23+24+…+22017=22018﹣1
以上解法,在数列求和中,我们称之为:“错位相减法”
请你根据上面的材料,解决下列问题
(1)求1+3+32+33+34+…+32019的值
(2)若a为正整数且![]() ,求
,求![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E在线段BC上,△ADE是等边三角形,且∠BAC=120°
(1)求证:△ABD∽△CAE;
(2)若BD=2,CE=8,求BC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com