
【题目】某校兴趣小组就“最想去的金华最美村落”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的最美乡村![]() 下面是根据调查结果绘制出的不完整的统计图
下面是根据调查结果绘制出的不完整的统计图
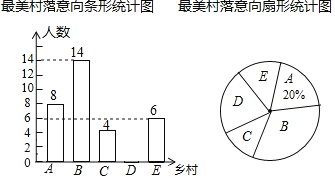
请根据图中提供的信息,解答下列问题:
![]() 被调查的学生总人数为______人;
被调查的学生总人数为______人;
![]() 扇形统计图中“最想去乡村D”的扇形圆心角的度数为______;
扇形统计图中“最想去乡村D”的扇形圆心角的度数为______;
![]() 若该校共有800名学生,请估计“最想去乡村B”的学生人数.
若该校共有800名学生,请估计“最想去乡村B”的学生人数.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在抛掷硬币的试验中,下列结论正确的是![]()
![]()
A. 经过大量重复的抛掷硬币试验,可发现“正面向上”的频率越来越稳定
B. 抛掷10000次硬币与抛掷12000次硬币“正面向上”的频率相同
C. 抛掷50000次硬币,可得“正面向上”的频率为![]()
D. 若抛掷2000次硬币“正面向上”的频率是![]() ,则“正面向下”的频率也为
,则“正面向下”的频率也为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | m | 93 | 93 | 12 |
九(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)直接写出表中m、n的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在研究“利用木板余料裁出最大面积的矩形”时发现:如图1,![]() 是一块直角三角形形状的木板余料
是一块直角三角形形状的木板余料![]() ,以
,以![]() 为内角裁一个矩形当DE,EF是中位线时,所裁矩形的面积最大
为内角裁一个矩形当DE,EF是中位线时,所裁矩形的面积最大![]() 若木板余料的形状改变,请你探究:
若木板余料的形状改变,请你探究:
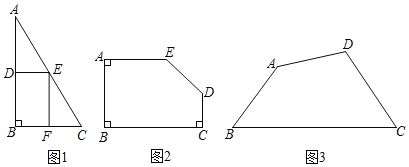
![]() 如图2,现有一块五边形的木板余料ABCDE,
如图2,现有一块五边形的木板余料ABCDE,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 现从中裁出一个以
现从中裁出一个以![]() 为内角且面积最大的矩形,则该矩形的面积为______
为内角且面积最大的矩形,则该矩形的面积为______![]() .
.
![]() 如图3,现有一块四边形的木板余料ABCD,经测量
如图3,现有一块四边形的木板余料ABCD,经测量![]() ,
,![]() ,
,![]() ,且
,且![]() ,从中裁出顶点M,N在边BC上且面积最大的矩形PQMN,则该矩形的面积为______
,从中裁出顶点M,N在边BC上且面积最大的矩形PQMN,则该矩形的面积为______![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在研究“利用木板余料裁出最大面积的矩形”时发现:如图1,![]() 是一块直角三角形形状的木板余料
是一块直角三角形形状的木板余料![]() ,以
,以![]() 为内角裁一个矩形当DE,EF是中位线时,所裁矩形的面积最大
为内角裁一个矩形当DE,EF是中位线时,所裁矩形的面积最大![]() 若木板余料的形状改变,请你探究:
若木板余料的形状改变,请你探究:
![]() 如图2,现有一块五边形的木板余料ABCDE,
如图2,现有一块五边形的木板余料ABCDE,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 现从中裁出一个以
现从中裁出一个以![]() 为内角且面积最大的矩形,则该矩形的面积为______
为内角且面积最大的矩形,则该矩形的面积为______![]() .
.
![]() 如图3,现有一块四边形的木板余料ABCD,经测量
如图3,现有一块四边形的木板余料ABCD,经测量![]() ,
,![]() ,
,![]() ,且
,且![]() ,从中裁出顶点M,N在边BC上且面积最大的矩形PQMN,则该矩形的面积为______
,从中裁出顶点M,N在边BC上且面积最大的矩形PQMN,则该矩形的面积为______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l上有两动点C、D,点A、点B在直线l同侧,且A点与B点分别到l的距离为a米和b米(即图中AA′=a米,BB′=b米),且A′B′=c米,动点CD之间的距离总为S米,使C到A的距离与D到B的距离之和最小,则AC+BD的最小值为( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
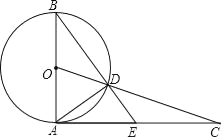
【题目】如图,AB是⊙O的直径,点C为⊙O外一点,连接OC交⊙O于点D,连接BD并延长交线段AC于点E,∠CDE=∠CAD.
(1)求证:CD2=ACEC;
(2)判断AC与⊙O的位置关系,并证明你的结论;
(3)若AE=EC,求tanB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
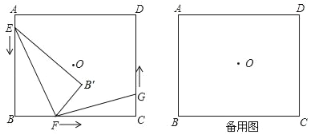
【题目】如图,点O为矩形ABCD的对称中心,AB=5cm,BC=6cm,点E.F.G分别从A.B.C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s,当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB′F.设点E.F.G运动的时间为t(单位:s).
(1)当t等于多少s时,四边形EBFB′为正方形;
(2)若以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;
(3)是否存在实数t,使得点B’与点O重合?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com