
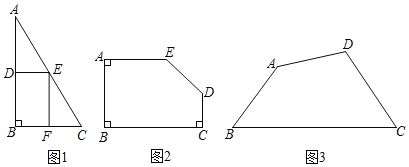
����Ŀ��С�����о�������ľ�����ϲó��������ľ�����ʱ���֣���ͼ1��![]() ��һ��ֱ����������״��ľ������
��һ��ֱ����������״��ľ������![]() ����
����![]() Ϊ�ڽDz�һ�����ε�DE��EF����λ��ʱ�����þ��ε�������
Ϊ�ڽDz�һ�����ε�DE��EF����λ��ʱ�����þ��ε�������![]() ��ľ�����ϵ���״�ı䣬����̽����
��ľ�����ϵ���״�ı䣬����̽����
![]() ��ͼ2������һ������ε�ľ������ABCDE��
��ͼ2������һ������ε�ľ������ABCDE��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ִ��вó�һ����
�ִ��вó�һ����![]() Ϊ�ڽ���������ľ��Σ���þ��ε����Ϊ______
Ϊ�ڽ���������ľ��Σ���þ��ε����Ϊ______![]() ��
��
![]() ��ͼ3������һ���ı��ε�ľ������ABCD��������
��ͼ3������һ���ı��ε�ľ������ABCD��������![]() ��
��![]() ��
��![]() ����
����![]() �����вó�����M��N�ڱ�BC����������ľ���PQMN����þ��ε����Ϊ______
�����вó�����M��N�ڱ�BC����������ľ���PQMN����þ��ε����Ϊ______![]() ��
��
���𰸡�400�� 486��
��������
��1����ͼ2�У��ӳ�AE��CD���ӳ�����F�����ı���ABCF�Ǿ��Σ�������ת��Ϊ�������ڽӾ��μ��ɽ�����⣮
��2���������κ��������ö��κ��������ʽ�����⼴�ɣ�
�⣺��1����ͼ2�У��ӳ�AE��CD���ӳ�����F�����ı���ABCF�Ǿ��Σ�
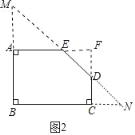
��AF��BC��30cm��AB��CF��20cm��
��AE��20cm��CD��10cm��
��EF��DF��10cm��
�ߡ�F��90����
���AEM����FED����FDE����CDN��45����
��AM��AE��20cm��CD��CN��10cm��
��BM��40cm��BN��40cm��
���BMN���ڽӾ��ε���������ֵ��20��20��400��cm2����
��2����ͼ3�У�
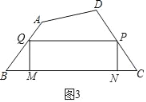
���ı���MNPQ�Ǿ��Σ�tanB��tanC��![]() ��
��
����Լ���QM��PN��4k��BM��CN��3k��
��MN��54��6 k��
��S����MNPQ��4k��54��6k������24��k��![]() ��2+486��
��2+486��
�ߩ�24��0��
��k��![]() ʱ������MNPQ�����������ֵΪ486��
ʱ������MNPQ�����������ֵΪ486��
��ʱBQ��PC��5k��![]() ���������⣬
���������⣬
�����MNPQ����������ֵΪ486cm2��
�ʴ�Ϊ400��486��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
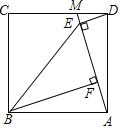
����Ŀ����ͼ����M��������ABCD��CD��һ�㣬����AM����DE��AM�ڵ�E��BF��AM�ڵ�F������BE��
��1����֤��AE=BF��
��2����֪AF=2���ı���ABED�����Ϊ24�����EBF������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڹ���С��Ʒ������ij־ԸС�����������룬����һ��ֻ�ᷭ�밢���������ֻ�ᷭ��Ӣ�����һ���������Զ��ᷭ��![]() �����������ѡ�������һ�飬������ܹ����������������Եĸ�����
�����������ѡ�������һ�飬������ܹ����������������Եĸ�����![]() ����
����![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��ͼ����x�ύ�ڵ�(-2��0)��(
��ͼ����x�ύ�ڵ�(-2��0)��(![]() )����
)����![]() ����y���������Ľ�����(0��2)���·��������н����У���ab>0����4a-2b+c=0����2a-b+1<0����a<b<c��������ȷ�Ľ�����( ).
����y���������Ľ�����(0��2)���·��������н����У���ab>0����4a-2b+c=0����2a-b+1<0����a<b<c��������ȷ�Ľ�����( ).
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
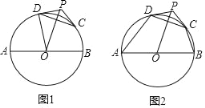
����Ŀ����ͼ1��AB�ǡ�O��ֱ����PΪ��O��һ�㣬C��DΪ��O�����㣬����OP��CD��PD��PC����֪AB��8��
��1����OP��5��PD��3����֤��PD�ǡ�O�����ߣ�
��2����PD��PC�ǡ�O�����ߣ�
����֤��OP��CD��
������AD��BC����ͼ2������DAB��50������CBA��70������CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ȤС���������ȥ�Ľ�������������������˱�У����ѧ����Ҫ��ÿλͬѧѡ����ֻ��ѡ��һ������ȥ���������![]() �����Ǹ��ݵ��������Ƴ��IJ�������ͳ��ͼ
�����Ǹ��ݵ��������Ƴ��IJ�������ͳ��ͼ
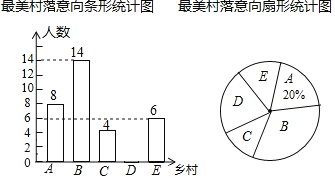
�����ͼ���ṩ����Ϣ������������⣺
![]() �������ѧ��������Ϊ______�ˣ�
�������ѧ��������Ϊ______�ˣ�
![]() ����ͳ��ͼ��������ȥ���D��������Բ�ĽǵĶ���Ϊ______��
����ͳ��ͼ��������ȥ���D��������Բ�ĽǵĶ���Ϊ______��
![]() ����У����800��ѧ���������������ȥ���B����ѧ��������
����У����800��ѧ���������������ȥ���B����ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ����У�װ�г���ɫ���������ͬ�ĺ졢����������֪���к�����3�����Ҵ�����������һ���Ǻ���ĸ���Ϊ0.75.
��1���������⣬������ ������.
��2������һ���������һ���Żأ�����������ڶ�����.���û���״ͼ���б�������������������һ����Ϊ����Ϊ�¼�A�����ĸ���P��A��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ί�ƻ���Ԫ���ڼ���֯������Ա������Ժȥ������ѡ����10��������Ա�μӷ�����������6�ˣ�Ů��4�ˣ�
![]() ������10�������ѡһ�˵��ӳ�����ѡ��Ů�����ӳ��ĸ��ʣ�
������10�������ѡһ�˵��ӳ�����ѡ��Ů�����ӳ��ĸ��ʣ�
![]() �־����Ӽס�����ѡһ�˵��ӳ�������������Ϸ�ķ�ʽ������˭���Σ���Ϸ�������£��������������ֱַ�Ϊ2��3��4��5���˿���ϴ�Ⱥ����ֳ��·������棬������ȡ2�ţ�����������֮��Ϊż������ѡ��Ϊ�ӳ�������ѡ��Ϊ�ӳ�
�־����Ӽס�����ѡһ�˵��ӳ�������������Ϸ�ķ�ʽ������˭���Σ���Ϸ�������£��������������ֱַ�Ϊ2��3��4��5���˿���ϴ�Ⱥ����ֳ��·������棬������ȡ2�ţ�����������֮��Ϊż������ѡ��Ϊ�ӳ�������ѡ��Ϊ�ӳ�![]() ���������Ϸ��ƽ��������״ͼ���б���˵�����ɣ�
���������Ϸ��ƽ��������״ͼ���б���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ���6��5��Ϊ���绷���գ�Ϊ���ᳫ��̼������ij��˾��������10̨��ʡ��Դ�����豸�����мס��������ͺŵ��豸�ɹ�ѡ��. �����飺����3̨�����豸�ȹ���2̨�����豸�16��Ԫ������2̨�����豸�ȹ���3̨�����豸�ٻ�6��Ԫ.
(1)��ס��������ͺ��豸�ļ۸�
(2)�ù�˾��Ԥ����������ʡ��Դ�����豸���ʽ���110��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
(3)�ڣ�2���������£���֪�����豸�IJ���Ϊ240��/�£������豸�IJ���Ϊ180��/��.��ÿ��Ҫ���ܲ���������2040�֣�Ϊ�˽�Լ�ʽ�����Ϊ�ù�˾���һ����ʡǮ�Ĺ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com