
【题目】已知二次函数![]() 的图像与x轴交于点(-2,0)、(
的图像与x轴交于点(-2,0)、(![]() ),且
),且![]() ,与y轴的正半轴的交点在(0,2)的下方,则下列结论中:①ab>0;②4a-2b+c=0;③2a-b+1<0;④a<b<c,其中正确的结论有( ).
,与y轴的正半轴的交点在(0,2)的下方,则下列结论中:①ab>0;②4a-2b+c=0;③2a-b+1<0;④a<b<c,其中正确的结论有( ).
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
根据已知画出图象,根据对称轴和开口方向可判断①;把x=-2代入得:4a-2b+c=0,可判断②;由②的结论,可得 2a-b=![]() ,根据c的取值范围可得2a-b的取值范围,可判断③;根据图象与x轴的交点可用x2表示对称轴,易确定a,b的取值范围,可判断④.
,根据c的取值范围可得2a-b的取值范围,可判断③;根据图象与x轴的交点可用x2表示对称轴,易确定a,b的取值范围,可判断④.
解:画出图象如图,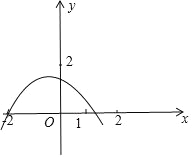
∵开口向下,
∴a<0,
∵x=![]() <0,
<0,
∴b<0,
∴ab>0,
∴①正确;
根据二次函数y=ax2+bx+c的图象与x轴交于点(2,0)、(x2,0),且1<x2<2,与y轴的正半轴的交点在(0,2)的下方,把x=2代入得:4a2b+c=0,
∴②正确;
由4a2b+c=0得2ab=![]() ,
,
而0<c<2,
∴1<![]() <0
<0
∴1<2ab<0
∴2ab+1>0,
∴③错误;
∵图象与x轴两交点为(2,0),(x2,0),且1<x2<2,
对称轴x=![]() =
=![]() ,
,
则对称轴![]() <
<![]() <0,且a<0,
<0,且a<0,
∴a>b
∴a<b<0,
由抛物线与y轴的正半轴的交点在(0,2)的下方,得c>0,
即a<b<c,
∴④正确;
所以正确的选项为①②④。
故选:C


科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x=﹣1的抛物线y=x2+bx+c与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).
(1)求点B的坐标;
(2)求二次函数的解析式;
(3)已知C为抛物线与y轴的交点,设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个含30°角的直角三角形ABC和直角三角形BED如图那样拼接,C、B、D在同一直线上,AC=BD,∠ABC=∠E=30°,∠ACB=∠BDE=90°,M为线段CB上一个动点(不与C、B重合).过M作MN⊥AM,交直线BE于N,过N作NH⊥BD于H.
(1)当M在什么位置时,△AMC∽△NBH?
(2)设AC=![]() .
.
①若CM=2,求BH的长;
②当M沿线段CB运动时,连接AN(图中未连),求△AMN面积的取值范围.
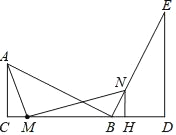
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | m | 93 | 93 | 12 |
九(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)直接写出表中m、n的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x(千米) | 8 | 9 | 10 | 11.5 | 13 |
y1(分钟) | 18 | 20 | 22 | 25 | 28 |
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间y2(单位:分钟)也受x的影响,其关系可以用y2=![]() x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在研究“利用木板余料裁出最大面积的矩形”时发现:如图1,![]() 是一块直角三角形形状的木板余料
是一块直角三角形形状的木板余料![]() ,以
,以![]() 为内角裁一个矩形当DE,EF是中位线时,所裁矩形的面积最大
为内角裁一个矩形当DE,EF是中位线时,所裁矩形的面积最大![]() 若木板余料的形状改变,请你探究:
若木板余料的形状改变,请你探究:
![]() 如图2,现有一块五边形的木板余料ABCDE,
如图2,现有一块五边形的木板余料ABCDE,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 现从中裁出一个以
现从中裁出一个以![]() 为内角且面积最大的矩形,则该矩形的面积为______
为内角且面积最大的矩形,则该矩形的面积为______![]() .
.
![]() 如图3,现有一块四边形的木板余料ABCD,经测量
如图3,现有一块四边形的木板余料ABCD,经测量![]() ,
,![]() ,
,![]() ,且
,且![]() ,从中裁出顶点M,N在边BC上且面积最大的矩形PQMN,则该矩形的面积为______
,从中裁出顶点M,N在边BC上且面积最大的矩形PQMN,则该矩形的面积为______![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在研究“利用木板余料裁出最大面积的矩形”时发现:如图1,![]() 是一块直角三角形形状的木板余料
是一块直角三角形形状的木板余料![]() ,以
,以![]() 为内角裁一个矩形当DE,EF是中位线时,所裁矩形的面积最大
为内角裁一个矩形当DE,EF是中位线时,所裁矩形的面积最大![]() 若木板余料的形状改变,请你探究:
若木板余料的形状改变,请你探究:
![]() 如图2,现有一块五边形的木板余料ABCDE,
如图2,现有一块五边形的木板余料ABCDE,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 现从中裁出一个以
现从中裁出一个以![]() 为内角且面积最大的矩形,则该矩形的面积为______
为内角且面积最大的矩形,则该矩形的面积为______![]() .
.
![]() 如图3,现有一块四边形的木板余料ABCD,经测量
如图3,现有一块四边形的木板余料ABCD,经测量![]() ,
,![]() ,
,![]() ,且
,且![]() ,从中裁出顶点M,N在边BC上且面积最大的矩形PQMN,则该矩形的面积为______
,从中裁出顶点M,N在边BC上且面积最大的矩形PQMN,则该矩形的面积为______![]() .
.
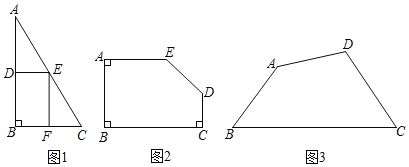
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O外一点,连接OC交⊙O于点D,连接BD并延长交线段AC于点E,∠CDE=∠CAD.
(1)求证:CD2=ACEC;
(2)判断AC与⊙O的位置关系,并证明你的结论;
(3)若AE=EC,求tanB的值.
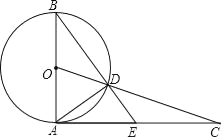
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=﹣![]() x2+
x2+![]() x+2
x+2![]() 与x轴交于A、B两点,与y轴交于C点,抛物线的顶点为Q,连接BC.
与x轴交于A、B两点,与y轴交于C点,抛物线的顶点为Q,连接BC.
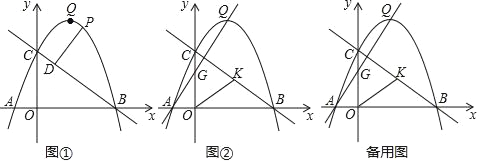
(1)求直线BC的解析式;
(2)点P是直线BC上方抛物线上的一点,过点P作PD⊥BC于点D,在直线BC上有一动点M,当线段PD最大时,求PM+![]() MB最小值;
MB最小值;
(3)如图②,直线AQ交y轴于G,取线段BC的中点K,连接OK,将△GOK沿直线AQ平移得△G′O'K′,将抛物线y=﹣![]() x2+
x2+![]() x+2
x+2![]() 沿直线AQ平移,记平移后的抛物线为y′,当抛物线y′经过点Q时,记顶点为Q′,是否存在以G'、K'、Q'为顶点的三角形是等腰三角形?若存在,求出点G′的坐标;若不存在,请说明理由.
沿直线AQ平移,记平移后的抛物线为y′,当抛物线y′经过点Q时,记顶点为Q′,是否存在以G'、K'、Q'为顶点的三角形是等腰三角形?若存在,求出点G′的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com