
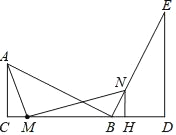
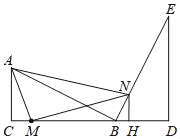
【题目】两个含30°角的直角三角形ABC和直角三角形BED如图那样拼接,C、B、D在同一直线上,AC=BD,∠ABC=∠E=30°,∠ACB=∠BDE=90°,M为线段CB上一个动点(不与C、B重合).过M作MN⊥AM,交直线BE于N,过N作NH⊥BD于H.
(1)当M在什么位置时,△AMC∽△NBH?
(2)设AC=![]() .
.
①若CM=2,求BH的长;
②当M沿线段CB运动时,连接AN(图中未连),求△AMN面积的取值范围.
【答案】(1)见解析;(2)①BH=2;②![]()
【解析】
(1)先确定△AMC和△NBH都是直角三角形,再根据垂直平行可得:∠BNH=30°,由相似三角形的对应关系,可得:当∠CAM=30°时,可得:△AMC∽△NBH,从而确定M的位置;
(2)①设BH=x,则HN=![]() ,MH=1+x,证明△ACM∽△MHN,则
,MH=1+x,证明△ACM∽△MHN,则![]() ,即
,即![]() ,可得BH的长;
,可得BH的长;
②由题得AC=BD=![]() ,BC=ED=3,∠NBH=60°,设CM=x(0<x<3),BH=t,则HN=
,BC=ED=3,∠NBH=60°,设CM=x(0<x<3),BH=t,则HN=![]() t,MB=3﹣x,从而MH=3﹣x+t,同理△ACM∽△MHN得列方程可得:BH=x,分别表示AM和MN的长,利用三角形面积公式可得S△AMN=
t,MB=3﹣x,从而MH=3﹣x+t,同理△ACM∽△MHN得列方程可得:BH=x,分别表示AM和MN的长,利用三角形面积公式可得S△AMN=![]() =
=![]() ,由x的取值范围可得结论.
,由x的取值范围可得结论.
解:(1)由题知,NH⊥BD,ED⊥BD,
∴∠BNH=30°,又△AMC与△NBH都是直角三角形,
∴当∠CAM=30°,即当M位于∠CAB的平分线上时,△AMC∽△NBH;
(2)①Rt△ACB中,∵AC=![]() ,CM=2,∠CAB=60°,
,CM=2,∠CAB=60°,
∴CB=3,MB=1,
设BH=x,
∵∠EBD=60°,
∴HN=![]() x,MH=1+x,
x,MH=1+x,
∵MN⊥AM,
∴∠AMC+∠NMH=90°,又∠AMC+∠CAM=90°,
∴∠CAM=∠HMN,
∵∠ACM=∠MHN=90°,
∴△ACM∽△MHN
∴![]() ,即
,即![]() ,x=2,即BH=2
,x=2,即BH=2
②由题得AC=BD=![]() ,BC=ED=3,∠NBH=60°,
,BC=ED=3,∠NBH=60°,
∴tan30°=![]() =
=![]() ,
,
设CM=x(0<x<3),BH=t,则HN=![]() t,MB=3﹣x,
t,MB=3﹣x,
从而MH=3﹣x+t,
由△ACM∽△MHN得![]() ,
,
(3﹣x)(t﹣x)=0,x<3,
∴t=x,即有BH=x,
MH=MB+BH=3﹣x+x=3,
AM=![]() ,MN=
,MN=![]() ,
,
S△AMN=![]()
=![]() ,
,
∴![]()


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
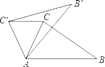
【题目】如图,△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB'C'的位置,使得C′C∥AB,则∠CAB'等于( )
A. 30°B. 25°C. 15°D. 10°
查看答案和解析>>
科目:初中数学 来源: 题型:
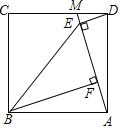
【题目】如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE.
(1)求证:AE=BF;
(2)已知AF=2,四边形ABED的面积为24,求∠EBF的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
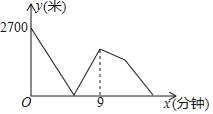
【题目】A,B两地之间有一条直线跑道,甲,乙两人分别从A,B同时出发,相向而行匀速跑步,且乙的速度是甲速度的80%,当甲,乙分别到达B地,A地后立即调头往回跑,甲的速度保持不变,乙的速度提高25%(仍保持匀速前行),甲,乙两人之间的距离y(米)与跑步时间x(分钟)之间的关系如图所示,则他们在第二次相遇时距B地_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
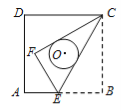
【题目】如图,正方形ABCD的边长为6,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
A.4![]() B.
B. ![]() C.
C.![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】义乌国际小商品博览会某志愿小组有五名翻译,其中一名只会翻译阿拉伯语,三名只会翻译英语,还有一名两种语言都会翻译![]() 若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是
若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像与x轴交于点(-2,0)、(
的图像与x轴交于点(-2,0)、(![]() ),且
),且![]() ,与y轴的正半轴的交点在(0,2)的下方,则下列结论中:①ab>0;②4a-2b+c=0;③2a-b+1<0;④a<b<c,其中正确的结论有( ).
,与y轴的正半轴的交点在(0,2)的下方,则下列结论中:①ab>0;②4a-2b+c=0;③2a-b+1<0;④a<b<c,其中正确的结论有( ).
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委计划在元且期间组织优秀团员到敬老院去服务,现选出了10名优秀团员参加服务,其中男生6人,女生4人.
![]() 若从这10人中随机选一人当队长,求选中女生当队长的概率;
若从这10人中随机选一人当队长,求选中女生当队长的概率;
![]() 现决定从甲、乙中选一人当队长,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则选甲为队长;否则,选乙为队长
现决定从甲、乙中选一人当队长,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则选甲为队长;否则,选乙为队长![]() 试问这个游戏公平吗?请用树状图或列表法说明理由.
试问这个游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com