
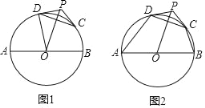
【题目】如图1,AB是⊙O的直径,P为⊙O外一点,C,D为⊙O上两点,连结OP,CD,PD=PC.已知AB=8.
(1)若OP=5,PD=3,求证:PD是⊙O的切线;
(2)若PD、PC是⊙O的切线;
①求证:OP⊥CD;
②连结AD,BC,如图2,若∠DAB=50°,∠CBA=70°,求弧CD的长.
【答案】(1)证明见解析;(2)①证明解析;②弧CD的长为![]() .
.
【解析】
1)利用勾股定理的逆定理证明∠DOP=90°即可.
(2)①如图1中,连接OC.由切线长定理可知PD=PC,因为OD=OC,所以OP垂直平分线段CD,由此即可解决问题.
②求出圆心角∠DOC的度数即可解决问题.
(1)证明:∵直径AB=8,
∴OD=4,
∵OP=5,PD=3,
∴OP2=PD2+OD2,
∴∠ODP=90°,
∴OD⊥DP,
∴PD是⊙O的切线.
(2)①证明:如图1中,连接OC.
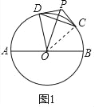
∵PD,PC是⊙O的切线,
∴PD=PC,
∵OD=OC,
∴OP垂直平分线段CD,
∴OP⊥CD.
②解:如图2中,连接OD,OC.
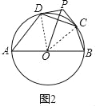
∵OA=OD,OB=OC,
∴∠A=∠ODA=50°,∠B=∠OCB=70°,
∴∠AOD=180°﹣100°=80°,∠BOC=180°﹣140°=40°,
∴∠DOC=180°﹣80°﹣40°=60°,
∴弧CD的长=![]() =
=![]() .
.
故答案为:(1)证明见解析;(2)①证明解析;②弧CD的长为![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
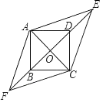
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE= ![]() ,∠EAF=135°,则以下结论正确的是( )
,∠EAF=135°,则以下结论正确的是( )
A. DE=1 B. tan∠AFO= ![]() C. AF=
C. AF= ![]() D. 四边形AFCE的面积为
D. 四边形AFCE的面积为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+2交x轴于点A(﹣2,0)、B,交y轴于点C;
(1)求抛物线的解析式;
(2)点P从点A出发,以1个单位/秒的速度向终点B运动,同时点Q从点C出发,以相同的速度沿y轴正方向向上运动,运动的时间为t秒,当点P到达点B时,点Q也停止运动,设△PQC的面积为S,求S与t间的函数关系式并直接写出t的取值范围;
(3)在(2)的条件下,当点P在线段OB上时,设PQ交直线AC于点G,过P作PE⊥AC于点E,求EG的长.
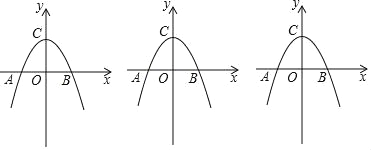
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x(千米) | 8 | 9 | 10 | 11.5 | 13 |
y1(分钟) | 18 | 20 | 22 | 25 | 28 |
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间y2(单位:分钟)也受x的影响,其关系可以用y2=![]() x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() ,
,![]() ,点P为AB边上的一个动点,点E、F分别是CA,CB边的中点,过点P作
,点P为AB边上的一个动点,点E、F分别是CA,CB边的中点,过点P作![]() 于D,设
于D,设![]() ,图中某条线段的长为y,如果表示y与x的函数关系的大致图象如图2所示,那么这条线段可能是
,图中某条线段的长为y,如果表示y与x的函数关系的大致图象如图2所示,那么这条线段可能是![]()
![]()
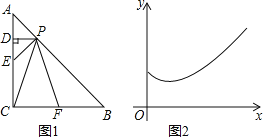
A. PDB. PEC. PCD. PF
查看答案和解析>>
科目:初中数学 来源: 题型:
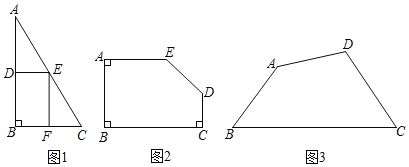
【题目】小明在研究“利用木板余料裁出最大面积的矩形”时发现:如图1,![]() 是一块直角三角形形状的木板余料
是一块直角三角形形状的木板余料![]() ,以
,以![]() 为内角裁一个矩形当DE,EF是中位线时,所裁矩形的面积最大
为内角裁一个矩形当DE,EF是中位线时,所裁矩形的面积最大![]() 若木板余料的形状改变,请你探究:
若木板余料的形状改变,请你探究:
![]() 如图2,现有一块五边形的木板余料ABCDE,
如图2,现有一块五边形的木板余料ABCDE,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 现从中裁出一个以
现从中裁出一个以![]() 为内角且面积最大的矩形,则该矩形的面积为______
为内角且面积最大的矩形,则该矩形的面积为______![]() .
.
![]() 如图3,现有一块四边形的木板余料ABCD,经测量
如图3,现有一块四边形的木板余料ABCD,经测量![]() ,
,![]() ,
,![]() ,且
,且![]() ,从中裁出顶点M,N在边BC上且面积最大的矩形PQMN,则该矩形的面积为______
,从中裁出顶点M,N在边BC上且面积最大的矩形PQMN,则该矩形的面积为______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数![]() (x>0)与正比例函数y=kx、
(x>0)与正比例函数y=kx、 ![]() (k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
(k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出的问题:只有一张电影票,小丽和小芳想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小丽和小芳都公平的方案.甲同学的方案:将红桃2、3、4、5四张牌背面向上,小丽先抽一张,小芳从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小丽看电影,否则小芳看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲同学的方案修改为只用2、3、5、7四张牌,抽取方式及规则不变,乙的方案公平吗?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com