
【题目】如图,在△![]() 中,∠
中,∠![]() ,点
,点![]() 是
是![]() 边上一点,以
边上一点,以![]() 为直径的⊙
为直径的⊙![]() 与边
与边![]() 相切于点
相切于点![]() ,与边
,与边![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ⊥
⊥![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
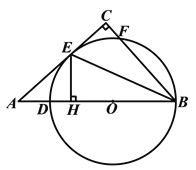
【答案】(1)证明见解析(2)![]()
【解析】分析:(1)连接OE.由切线的性质得到OE⊥AC,从而有OE∥BC,由平行线的性质得到∠OEB=∠CBE.再由等腰三角形的性质得到∠OEB=∠OBE,即有∠OBE=∠CBE,由角平分线的性质即可得出结论;
(2)解Rt△ABC得到AB的长.再由OE∥BC,得到△AEO∽△ACB,由相似三角形对应边成比例,得到OB的长,进而可得出结论.
详解:(1)连接OE.
∵⊙O与边AC相切,∴OE⊥AC.
∵∠C=90°,∴OE∥BC,∴∠OEB=∠CBE.
∵OB=OE,∴∠OEB=∠OBE,∴∠OBE=∠CBE.
∵EH⊥AB,∴EH=EC.
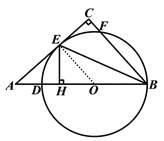
(2)在Rt△![]() 中,
中,![]() ,∴
,∴![]() .
.
∵![]() ∥
∥![]() ,∴△AEO∽△ACB,
,∴△AEO∽△ACB,
∴![]() ,即
,即![]() .
.
解得:![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校兴趣小组就“最想去的金华最美村落”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的最美乡村![]() 下面是根据调查结果绘制出的不完整的统计图
下面是根据调查结果绘制出的不完整的统计图
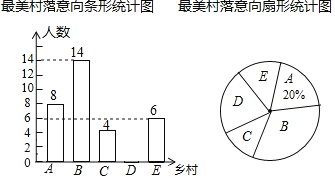
请根据图中提供的信息,解答下列问题:
![]() 被调查的学生总人数为______人;
被调查的学生总人数为______人;
![]() 扇形统计图中“最想去乡村D”的扇形圆心角的度数为______;
扇形统计图中“最想去乡村D”的扇形圆心角的度数为______;
![]() 若该校共有800名学生,请估计“最想去乡村B”的学生人数.
若该校共有800名学生,请估计“最想去乡村B”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
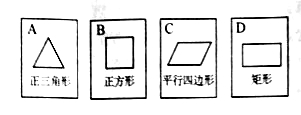
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委计划在元且期间组织优秀团员到敬老院去服务,现选出了10名优秀团员参加服务,其中男生6人,女生4人.
![]() 若从这10人中随机选一人当队长,求选中女生当队长的概率;
若从这10人中随机选一人当队长,求选中女生当队长的概率;
![]() 现决定从甲、乙中选一人当队长,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则选甲为队长;否则,选乙为队长
现决定从甲、乙中选一人当队长,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则选甲为队长;否则,选乙为队长![]() 试问这个游戏公平吗?请用树状图或列表法说明理由.
试问这个游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题:
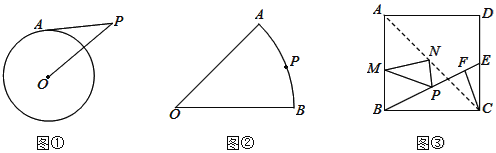
![]() 如图
如图![]() ,半径为4的
,半径为4的![]() 外有一点P,且
外有一点P,且![]() ,点A在
,点A在![]() 上,则PA的最大值和最小值分别是______和______.
上,则PA的最大值和最小值分别是______和______.
![]() 如图
如图![]() ,扇形AOB的半径为4,
,扇形AOB的半径为4,![]() ,P为弧AB上一点,分别在OA边找点E,在OB边上找一点F,使得
,P为弧AB上一点,分别在OA边找点E,在OB边上找一点F,使得![]() 周长的最小,请在图
周长的最小,请在图![]() 中确定点E、F的位置并直接写出
中确定点E、F的位置并直接写出![]() 周长的最小值;
周长的最小值;
拓展应用
![]() 如图
如图![]() ,正方形ABCD的边长为
,正方形ABCD的边长为![]() ;E是CD上一点
;E是CD上一点![]() 不与D、C重合
不与D、C重合![]() ,
,![]() 于F,P在BE上,且
于F,P在BE上,且![]() ,M、N分别是AB、AC上动点,求
,M、N分别是AB、AC上动点,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22017
首先设S=1+2+22+23+24+…+22017 ① 则2S=2+22+23+24+25+…+22018 ②
②﹣①得S=22018﹣1 即1+2+22+23+24+…+22017=22018﹣1
以上解法,在数列求和中,我们称之为:“错位相减法”
请你根据上面的材料,解决下列问题
(1)求1+3+32+33+34+…+32019的值
(2)若a为正整数且![]() ,求
,求![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
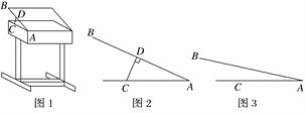
【题目】某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30 cm.
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长;
(2)如图3,当∠BAC=12°时,求AD的长.(结果保留根号)
(参考数据:sin 24°≈0.40,cos 24°≈0.91,tan 24°≈0.46,sin 12°≈0.20)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com