
����Ŀ���Ķ�������龰�Ի���Ȼ�������⣺
��ʦ�����Ƕ���һ�������Σ�����ƽ���͵��ڵ�����ƽ����2���������ν�������������.
С�����ȱ�������һ��������������!
С������ֱ�����������Ƿ����������������?
����(1)���������������������Ķ��壬�����ж�С������IJ��룺���ȱ�������һ�����������������Ƿ���ȷ?__________.(����������������)
����(2)����֪Rt��ABC�У����߳��ֱ���![]() ��10��������������������������Σ����������__________.
��10������������������������������������__________.
����(3)����ͼ����ABΪб�߷ֱ���AB��������ֱ�������Σ���AD=BD�����ı���ADBC�ڴ��ڵ�E��ʹ��AE=AD��CB=CE.��˵������ACE������������.

���𰸡���1���ǣ���2��5![]() ����3��������
����3��������
��������
���⣨1�������������������������εĶ���ֱ�ӽ����жϼ��ɣ�
���⣨2����c��б�ߺ�b��б������������ٸ��ݹ��ɶ����жϳ��������������Ƿ�������������εĶ��壮
���⣨3�����ù��ɶ�����AC2+BC2=AB2��AD2+BD2=AB2����AD=BD����AD=BD������2AD2=AB2������AE=AD��CB=CE������AC2+CE2=2AE2��Ȼ������¶��弴���ж���ACE�����������Σ�
��1���⣺��ȱ������ε�һ��Ϊa����a2+a2=2a2��
�������������������Ķ��壮
�ࡰ�ȱ�������һ������������������ȷ��
�ʴ�Ϊ���ǣ�
��2���⣺����10Ϊб��ʱ����һ��ֱ�DZ�=![]() =5
=5![]() ��
��
����![]() ��2+��
��2+��![]() ��2��2��102����
��2��2��102����![]() ��2+102��2����
��2+102��2����![]() ��2����
��2����
��Rt��ABC��������������
����![]() ��10��ֱ�DZ�ʱ��б��=
��10��ֱ�DZ�ʱ��б��=![]() =5
=5![]() ��
��
����![]() ��2+��5
��2+��5![]() ��2=200
��2=200
��2��102=200
����5![]() ��2+��5
��2+��5![]() ��2=2��102
��2=2��102
��Rt��ABC������������
�ʴ�Ϊ5![]() ��
��
��3��֤�����ߡ�ACB=��ADB=90����
��AC2+BC2=AB2��AD2+BD2=AB2��
��AD=BD��
��2AD2=AB2��
��AE=AD��CB=CE��
��AC2+CE2=2AE2��
���ACE������������


 �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д� �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
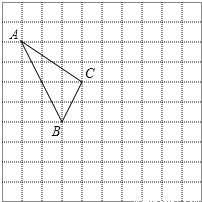
����Ŀ������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊ1����������Σ������������ߵĽ���������Σ�ABC�Ķ���A��C������ֱ�Ϊ����4��5��������1��3����
��1��������ͼ��ʾ������ƽ��������ƽ��ֱ������ϵ��
��2�����B��������
��3������ABC����ƽ��5����λ���ȣ�����ƽ��2����λ���ȣ�����ƽ�ƺ��ͼ�Ρ�A��B��C�䣻
��4�������A��B��C�������q
��5����x���ϴ���һ��P��ʹPA+PC��С��ֱ��д����P������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ������� ABC �ı߳�Ϊ 3������ B ��ֱ�� l��AB���ҡ�ABC ����A��BC������ֱ�� l �Գ���D Ϊ�߶� BC����һ���㣬�� AD+CD ����Сֵ��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У������Խ����ཻ�ڵ�O��AEƽ�֡�BAD����BC���ϵ��е�E������OE�����н��ۣ��١�ACB=30�㣻��OE��BC����OE=![]() BC����S��ACE=
BC����S��ACE=![]() SABCD��������ȷ�ĸ����ǣ�������
SABCD��������ȷ�ĸ����ǣ�������

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪ƽ���ı���ABCD���Խ���AC��BD�ཻ�ڵ�O����OBC=��OCB��
��1����֤��ƽ���ı���ABCD�Ǿ��Σ�
��2��������һ������ʹ����ABCDΪ�����Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ijͬѧ��һ�������εIJ�������������飬����Ҫ��������ȥ��һ����ȫһ���IJ�������ô��ʡ�µİ취�ǣ� ��

A.����ȥB.����ȥC.����ȥD.���ٺ͢�ȥ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ABC�У���֪AB=AC,DΪ�ױ�BC�ϵ�һ�㣬EΪ�߶�AD�ϵ�һ�㣬�ҡ�BED=��BAC=2��DEC������CE.
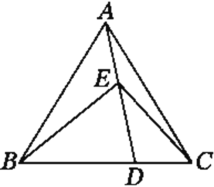
��1����֤����ABE=��DAC
��2������BAC=60�������ж�BD��CD��������������ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
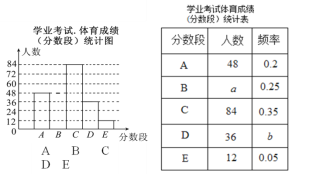
����Ŀ��Ϊ�˽�ij�о��꼶ѧ��ѧҵ���������ɼ����ִ��������ȡ����ѧ���������ɼ����зֶΣ�A��50�֣�B��49��45�֣�C��44��40�֣�D��39��30�֣�E��29��0�֣�ͳ�����£����������ṩ����Ϣ���ش��������⣺
��1��a��ֵΪ_ _��b��ֵΪ _ _������ͳ��ͼ����������
��2����ͬѧ˵�����ҵ������ɼ��Ǵ˴γ��������������ݵ���λ��������ͬѧ�������ɼ�Ӧ��ʲô�������ڣ�
��3�����ɼ���40�����ϣ���40�֣�)Ϊ���㣬���Ƹ��н���10440�����꼶ѧ���������ɼ�Ϊ�����ѧ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ת����ת�̱�![]() �ȷ֣�ָ������ÿ�������ڵĻ�����ȣ�
�ȷ֣�ָ������ÿ�������ڵĻ�����ȣ�
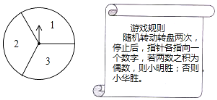
![]() �����ת��ת��һ�Σ�ֹͣ��ָ��ָ������
�����ת��ת��һ�Σ�ֹͣ��ָ��ָ������![]() �ĸ���Ϊ________��
�ĸ���Ϊ________��
![]() С����С���������ת������Ϸ��������������Ϸ��������Ϊ��˫����ƽ�������б�����״ͼ�ķ���˵�����ɣ�
С����С���������ת������Ϸ��������������Ϸ��������Ϊ��˫����ƽ�������б�����״ͼ�ķ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com