
【题目】如图可以自由转动的转盘被![]() 等分,指针落在每个扇形内的机会均等.
等分,指针落在每个扇形内的机会均等.
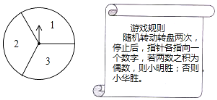
![]() 现随机转动转盘一次,停止后,指针指向数字
现随机转动转盘一次,停止后,指针指向数字![]() 的概率为________;
的概率为________;
![]() 小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.
小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的情景对话,然后解答问题:
老师:我们定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小华:等边三角形一定是奇异三角形!
小明:那直角三角形中是否存在奇异三角形呢?
问题(1):根据“奇异三角形”的定义,请你判断小华提出的猜想:“等边三角形一定是奇异三角形”是否正确?__________.(填“是”或“否”)
问题(2):已知RtΔABC中,两边长分别是![]() ,10,,若这个三角形是奇异三角形,则第三边是__________.
,10,,若这个三角形是奇异三角形,则第三边是__________.
问题(3):如图,以AB为斜边分别在AB的两侧作直角三角形,且AD=BD,若四边形ADBC内存在点E,使得AE=AD,CB=CE.试说明:△ACE是奇异三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
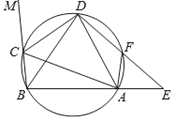
【题目】如图,在圆内接四边形ABCD中,CD为△BAC的外角平分线,F为弧AD上一点,BC=AF,延长DF与BA的延长线交于E.
(1)求证:AD=BD;
(2)若AC=10,AF=3,DF:FE=3:2,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知Rt△AOB的两条直角边0A、08分别在y轴和x轴上,并且OA、OB的长分别是方程x2—7x+12=0的两根(OA<0B),动点P从点A开始在线段AO上以每秒l个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.
(1)求A、B两点的坐标。
(2)求当t为何值时,△APQ与△AOB相似,并直接写出此时点Q的坐标.
(3)当t=2时,在坐标平面内,是否存在点M,使以A、P、Q、M为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.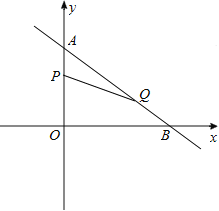
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,根据图象回答:
的图象如图所示,根据图象回答:
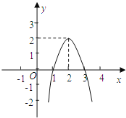
![]() 当
当![]() 时,写出自变量
时,写出自变量![]() 的值.
的值.
![]() 当
当![]() 时,写出自变量
时,写出自变量![]() 的取值范围.
的取值范围.
![]() 写出
写出![]() 随
随![]() 的增大而减小的自变量
的增大而减小的自变量![]() 的取值范围.
的取值范围.
![]() 若方程
若方程![]() 有两个不相等的实数根,求
有两个不相等的实数根,求![]() 的取值范围(用含
的取值范围(用含![]() 、
、![]() 、
、![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,连接
上,连接![]() ,
,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() ,
,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() .
.
![]() 求证:四边形
求证:四边形![]() 是矩形.
是矩形.
![]() 小明在完成
小明在完成![]() 的证明后继续进行了探索,过点
的证明后继续进行了探索,过点![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,得到四边形
,得到四边形![]() .此时,他猜想四边形
.此时,他猜想四边形![]() 是菱形.请在下列框图中补全他的证明思路.
是菱形.请在下列框图中补全他的证明思路.
小明的证明思路:由![]() ,
,![]() ,
,![]() 易证,四边形
易证,四边形![]() 是平行四边形.要证□
是平行四边形.要证□![]() 是菱形,只要证
是菱形,只要证![]() .由已知条件________,
.由已知条件________,![]() ,可证
,可证![]() ,故只要证
,故只要证![]() ,即证
,即证![]() ,易证________,________,故只要证
,易证________,________,故只要证![]() ,易证
,易证![]() ,
,![]() ,________,故得
,________,故得![]() ,即可得证.
,即可得证.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏果超市用5000元购进一批新品种的苹果进行试销,由于试销状况良好,超市又调拨11000元资金购进该种苹果,但这次的进价比试销时每千克多了0.5元,购进苹果的数量是试销时的2倍。
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种的苹果按每千克7元定价出售,当大部分苹果售出后,余下的400千克按定价的七折售完,那么超市在这两次苹果销售中共盈利多少元?(7分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com