
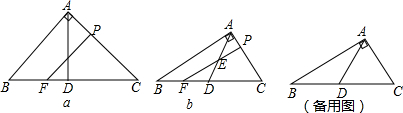
分析 (1)由已知条件得到△APE和△PFC是等腰直角三角形,根据等腰直角三角形的性质即可得到结果;
(2)猜想PE+PF=AB,①如图1,作FH⊥AB于点H,得到四边形AHFP为矩形,于是得到AH=PF,AP=HF,由AD为斜边BC的中点,得到AD=BD=$\frac{1}{2}$BC,∠B=∠BAD,根据平行线的性质得到∠AEP=∠BAD,证得△AEP≌△FBH,于是结论可得;②不成立,当点P在AC延长线时,AB=PE-PF,当点P在CA延长线时,AB=PF-PE.
解答 解:(1)∵∠BAC=90°,AB=AC=5,
∴∠C=45°,
∵PF∥AB,
∴∠FPC=∠BAC=90°,
∴PF=PC,
∵AP=2,
∴PF=PC=3,∵∠EPA=∠BAC=90°,
∵D为斜边BC的中点,
∴∠EAP=45°,
∴PE=PA=2;
(2)猜想PE+PF=AB,
①如图1,作FH⊥AB于点H,
∴∠AHF=90°,
∵∠BAC=90°,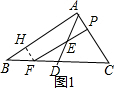
又∵PF∥AB
∴∠APF=∠HAP=90°,
∴四边形AHFP为矩形,
∴AH=PF,AP=HF,
∵AD为斜边BC的中点,
∴AD=BD=$\frac{1}{2}$BC,∴∠B=∠BAD,
∵PF∥AB,
∴∠AEP=∠BAD,
∴∠AEP=∠B,在△AEP与△FBH中,$\left\{\begin{array}{l}{∠APE=∠BHF}\\{∠AEP=∠B}\\{AP=HF}\end{array}\right.$,
∴△AEP≌△FBH,
∴PE=HB,
∵AB=AH+BH,
∴AB=PE+PF,
②不成立,当点P在AC延长线时,AB=PE-PF,
如图2,作FH⊥AB于点H,
∴∠AHF=90°,
∵∠BAC=90°
又∵PF∥AB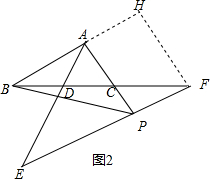
∴∠APF=∠HAP=90°,
∴四边形AHFP为矩形,
∴AH=PF,AP=HF,
∵AD为斜边BC的中点,
∴AD=BD=$\frac{1}{2}$BC,∴∠ABC=∠BAD,
∵PF∥AB,
∴∠AEP=∠BAD,
∴∠AEP=∠B,
在△AEP与△FBH中,$\left\{\begin{array}{l}{∠APE=∠BHF}\\{∠AEP=∠B}\\{AP=HF}\end{array}\right.$,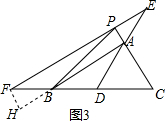
∴△AEP≌△FBH,
∴PE=HB,
∴AB=HB-AH=PE-PF;
当点P在CA延长线时,AB=PF-PE.
如图3,作FH⊥AB于点H,
∴四边形AHFP为矩形,
∴FH=AP,
同理△AEP≌△FBH,
∴PE=HB,
∴AB=AH-HB=PF-PE.
点评 本题考查了全等三角形的判定和性质,平行线的性质,等腰直角三角形的性质,正确的作出辅助线构造矩形是解题的关键.


科目:初中数学 来源: 题型:解答题
| 上市时间x天 | 4 | 10 | 36 |
| 市场价y元 | 90 | 51 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
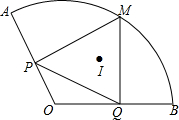 如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )
如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )| A. | 1≤MI≤$\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$≤MI≤1 | C. | $\frac{1}{2}$≤MI≤$\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$-1≤MI≤1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( )
如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( )| A. | CD+DF=4 | B. | CD-DF=2$\sqrt{3}$-3 | C. | BC+AB=2$\sqrt{3}$+4 | D. | BC-AB=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 63×104 | B. | 6.3×105 | C. | 6.3×1012 | D. | 6.3×1013 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等边三角形既是轴对称图形又是中心对称图形 | |
| B. | 两条对角线互相垂直且平分的四边形是正方形 | |
| C. | 有一个角是60°的等腰三角形是等边三角形 | |
| D. | 有两条对角线相等的四边形是矩形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com