
 如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( )
如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( )| A. | CD+DF=4 | B. | CD-DF=2$\sqrt{3}$-3 | C. | BC+AB=2$\sqrt{3}$+4 | D. | BC-AB=2 |
分析 设⊙O与BC的切点为M,连接MO并延长MO交AD于点N,证明△OMG≌△GCD,得到OM=GC=1,CD=GM=BC-BM-GC=BC-2.设AB=a,BC=b,AC=c,⊙O的半径为r,⊙O是Rt△ABC的内切圆可得r=$\frac{1}{2}$(a+b-c),所以c=a+b-2.在Rt△ABC中,利用勾股定理求得${a}_{1}=1+\sqrt{3},{a}_{2}=1-\sqrt{3}$(舍去),从而求出a,b的值,所以BC+AB=2$\sqrt{3}$+4.再设DF=x,在Rt△ONF中,FN=$3+\sqrt{3}-1-x$,OF=x,ON=$1+\sqrt{3}-1=\sqrt{3}$,由勾股定理可得$(2+\sqrt{3}-x)^{2}+(\sqrt{3})^{2}={x}^{2}$,解得x=4$-\sqrt{3}$,从而得到CD-DF=$\sqrt{3}+1-(4-\sqrt{3})=2\sqrt{3}-3$,CD+DF=$\sqrt{3}+1+4-\sqrt{3}=5$.即可解答.
解答 解:如图,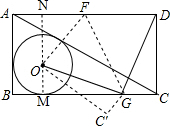
设⊙O与BC的切点为M,连接MO并延长MO交AD于点N,
∵将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG,
∴OG=DG,
∵OG⊥DG,
∴∠MGO+∠DGC=90°,
∵∠MOG+∠MGO=90°,
∴∠MOG=∠DGC,
在△OMG和△GCD中,
$\left\{\begin{array}{l}{∠OMG=∠DCG=9{0}^{°}}\\{∠MOG=∠DGC}\\{OG=DG}\end{array}\right.$
∴△OMG≌△GCD,
∴OM=GC=1,CD=GM=BC-BM-GC=BC-2.
∵AB=CD,
∴BC-AB=2.
设AB=a,BC=b,AC=c,⊙O的半径为r,
⊙O是Rt△ABC的内切圆可得r=$\frac{1}{2}$(a+b-c),
∴c=a+b-2.
在Rt△ABC中,由勾股定理可得a2+b2=(a+b-2)2,
整理得2ab-4a-4b+4=0,
又∵BC-AB=2即b=2+a,代入可得2a(2+a)-4a-4(2+a)+4=0,
解得${a}_{1}=1+\sqrt{3},{a}_{2}=1-\sqrt{3}$(舍去),
∴$a=1+\sqrt{3},b=3+\sqrt{3}$,
∴BC+AB=2$\sqrt{3}$+4.
再设DF=x,在Rt△ONF中,FN=$3+\sqrt{3}-1-x$,OF=x,ON=$1+\sqrt{3}-1=\sqrt{3}$,
由勾股定理可得$(2+\sqrt{3}-x)^{2}+(\sqrt{3})^{2}={x}^{2}$,
解得x=4$-\sqrt{3}$,
∴CD-DF=$\sqrt{3}+1-(4-\sqrt{3})=2\sqrt{3}-3$,CD+DF=$\sqrt{3}+1+4-\sqrt{3}=5$.
综上只有选项A错误,
故选A.
点评 本题考查了三角形的内切圆和内心,切线的性质,勾股定理,矩形的性质等知识点的综合应用,解决本题的关键是三角形内切圆的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.368×10 | B. | 13.68×1010 | C. | 1.368×1011 | D. | 1.368×1012 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com