
分析 (1)仿照以上方法求出原式的值即可;
(2)根据题示规律等式右边为十位数的积与个位数和的100倍加上个位数的平方,列式表示即可,验证可根据整式乘法展开结合十位数字和为10变形可得;
(3)类比(2)中方法4918×5118=10000×(49×51+18)+182,验算过程可将4918×5118写成(49×100+18)(51×100+18)后展开、合并可得,
推广到任意具有相同规律的四位数,分别用a,b表示两个四位数的千位和百位组成的两位数,用c表示两个四位数上个位和十位组成的两位数,且a+b=100,则(100a+c)(100b+c)=10000(ab+c)+c2,验证可参照上述做法.
解答 解:(1)77×37=100×(7×3+7)+72=2849;
(2)(10a+c)(10b+c)=100(ab+c)+c2,其中a+b=10,
证明:左边=100ab+10ac+10bc+c2
=100ab+10c(a+b)+c2
=100ab+100c+c2
=100(ab+c)+c2=右边,
故(10a+c)(10b+c)=100(ab+c)+c2,其中a+b=10,成立;
(3)4918×5118=(49×100+18)(51×100+18)
=49×51×10000+49×100×18+51×100×18+182
=10000×49×51+100×18×(49+51)+182
=10000×49×51+10000×18+182
=10000×(49×51+18)+182,
即4918×5118=10000×(49×51+18)+182
分别用a,b表示两个四位数的千位和百位组成的两位数,用c表示两个四位数上个位和十位组成的两位数,且a+b=100,
则(100a+c)(100b+c)=10000ab+100ac+100bc+c2
=10000ab+100c(a+b)+c2
=10000ab+10000c+c2
=10000(ab+c)+c2
即(100a+c)(100b+c)=10000(ab+c)+c2.
点评 本题主要考查整式的混合运算和数字的计算规律,寻找计算规律是前提,并加以运用和推广是关键,主要考查了数学的类比思想,整式的运算是解题的基础.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 开口方向向上,y有最小值是-2 | B. | 抛物线与x轴有两个交点 | ||
| C. | 顶点坐标是(-1,-2) | D. | 当x<1时,y随x增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知反比例函数y=$\frac{k}{x}$(k≠0)的图象过点A(-3,2).
如图,已知反比例函数y=$\frac{k}{x}$(k≠0)的图象过点A(-3,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,则所得任一多边形内角和度数不可能是( )
如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,则所得任一多边形内角和度数不可能是( )| A. | 720° | B. | 540° | C. | 360° | D. | 180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
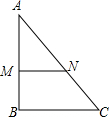 如图,在△ABC中,AC=10,AB=8,直线l分别与AB,AC交于M,N两点,且l∥BC,若S△AMN:S△ABC=4:9,则AM+AN的长为( )
如图,在△ABC中,AC=10,AB=8,直线l分别与AB,AC交于M,N两点,且l∥BC,若S△AMN:S△ABC=4:9,则AM+AN的长为( )| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com