
����Ŀ����ͼ����֪���κ�����ͼ����A��4��4����B��5��0����ԭ��O��PΪ���κ���ͼ���ϵ�һ�����㣬����P��x��Ĵ��ߣ�����ΪD��m��0��������ֱ��OA���ڵ�C��
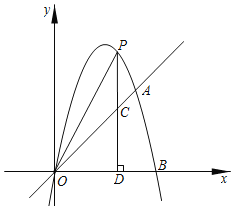
��1��������κ����Ľ���ʽ��
��2������P��ֱ��OA���Ϸ�ʱ�����߶�PC�����ֵ��
��3����m��0ʱ��̽���Ƿ���ڵ�P��ʹ�á�PCOΪ���������Σ�������ڣ����P�����ꣻ��������ڣ���˵�����ɣ�
���𰸡���1��y����x2+5x����2������P��ֱ��OA���Ϸ�ʱ���߶�PC�����ֵ��4����3�����ڣ�P�������ǣ�4��![]() ��2+3
��2+3![]() ����4+
����4+![]() ��2��3
��2��3![]() ����6����6����5��0����
����6����6����5��0����
��������
��1����y��ax��x��5������A��������뼴������𰸣�
��2�����ݵ���������PC����m2+4m�����ɶ���ʽ��������߶�PC�����ֵ��
��3����0��m��4ʱ������OC��PC���г����̣�������̵Ľ⼴�ɣ���m��4ʱ��PC��CD��PD��m2��4m��OC��![]() m����Ϊ����������ٵ�OC��PCʱ��m2��4m��
m����Ϊ����������ٵ�OC��PCʱ��m2��4m��![]() m��������̵Ľ⼴�ɵõ�P�����ꣻͬ�����ڵ�OC��OPʱ���۵�PC��OPʱ����P�����꣮�ۺ��������ɵõ��𰸣�
m��������̵Ľ⼴�ɵõ�P�����ꣻͬ�����ڵ�OC��OPʱ���۵�PC��OPʱ����P�����꣮�ۺ��������ɵõ��𰸣�
�⣺��1����y��ax��x��5����
��A�����꣨4��4������ã�4a��4��5����4��
���a����1��
�����Ľ���ʽΪy����x2+5x��
�𣺶��κ����Ľ���ʽ��y����x2+5x��
��2���⣺0��m��4��PC��PD��CD��
��D��m��0����PD��x�ᣬP��y����x2+5x�ϣ�C��ֱ��OA�ϣ�A��4��4����
��P��m����m2+5m����C��m��m��
��PC��PD��CD����m2+5m��m����m2+4m��
������m��2��2+4��
��a����1��0���������£�
�������ֵ��
��D��2��0��ʱ��PCmax��4��
�𣺵���P��ֱ��OA���Ϸ�ʱ���߶�PC�����ֵ��4��
��3����0��m��4ʱ������OC��PC���ੁm2+4m��![]() m��
m��
���m��4��![]() ��
��
��P��4��![]() ��2+3
��2+3![]() ����
����
��m��4ʱ��PC��CD��PD��m2��4m��OC��![]() m��
m��
�ɹ��ɶ����ã�OP2��OD2+DP2��m2+m2��m��5��2��
�ٵ�OC��PCʱ��m2��4m��![]() m��
m��
��ã�m��4+![]() ��m��0����ȥ����
��m��0����ȥ����
��P��4+![]() ��2��3
��2��3![]() ����
����
�ڵ�OC��OPʱ����![]() m��2��m2+m2��m��5��2��
m��2��m2+m2��m��5��2��
��ã�m1��6��m2��4��
��m��4ʱ��P��A�غϣ���P��C�غϣ�������ɡ�POC��
��m��4��ȥ��
��P��6����6����
�۵�PC��OPʱ��m2��m��4��2��m2+m2��m��5��2��
��ã�m��5��
��P��5��0����
�𣺴��ڣ�P�������ǣ�4��![]() ��2+3
��2+3![]() ����4+
����4+![]() ��2��3
��2��3![]() ����6����6����5��0����
����6����6����5��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��![]() �뷴��������
�뷴��������![]() ��ͼ��ֱ��ڵ�
��ͼ��ֱ��ڵ�![]() �͵�
�͵�![]() ����������ֱ��ڵ�
����������ֱ��ڵ�![]() �͵�
�͵�![]() .����
.����![]() ��
��![]() ����һ���㣬��
����һ���㣬��![]() ��
��![]() ����ʱ�����
����ʱ�����![]() ������Ϊ______.
������Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����У�ֱ���һ��һŮ��4����ʦ������ũ����ѧ֧�̣�
��1�����Ӽס�����У�����Ľ�ʦ�зֱ����ѡ1��������ѡ��2����ʦ�Ա���ͬ�ĸ����� ��
��2�����ӱ�����4����ʦ�����ѡ2�������б�����״ͼ�ķ��������2����ʦ����ͬһ��ѧУ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ����з������ŷֱ�д������1��2��3��4�ĺ�ɫ��Ƭ�����ŷֱ�д������1��2��3����ɫ��Ƭ����Ƭ����ɫ��������������ȫ��ͬ��
��1�����������ȡһ�ſ�Ƭ����ÿ�Ƭ��д������1�ĸ����ǣ�
��2����3����ɫ��Ƭȡ�����������һ�������ĺ����ڣ�Ȼ�������������ڸ������ȡһ�ſ�Ƭ���Ժ�ɫ��Ƭ�ϵ�������Ϊʮλ������ɫ��Ƭ�ϵ�������Ϊ��λ�����һ����λ�����������λ������22�ĸ���������������״ͼ���б���˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
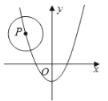
����Ŀ����ͼ����֪��P�İ뾶Ϊ4��Բ��P��������y��x2��2x��3���˶�������P��x������ʱ����Բ��P������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC�Ķ���O������ԭ���غϣ���߳�Ϊ2����A����C�ֱ���![]() �ᣬ
�ᣬ![]() ����������ϣ�����
����������ϣ�����![]() ��ͼ����CB���ڵ�D������
��ͼ����CB���ڵ�D������![]() ��
��![]() ������
Ϊ������![]() ����ͼ����D����AB���ڵ�E���뺯��
����ͼ����D����AB���ڵ�E���뺯��![]() ��ͼ���ڵ��������ڽ��ڵ�F������AF��EF��
��ͼ���ڵ��������ڽ��ڵ�F������AF��EF��

��1������![]() �ı���ʽ����ֱ��д��E��F��������꣮
�ı���ʽ����ֱ��д��E��F��������꣮
��2������AEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵxOy�еĵ�P����C���������¶��壺����C�ϴ���������A��B��ʹ����APB=60�������PΪ��C �Ĺ����㡣��֪��D��![]() ��
��![]() ����E��0����2����F��
����E��0����2����F��![]() ��0��
��0��
��1������O�İ뾶Ϊ1ʱ��
���ڵ�D��E��F�У���O�Ĺ������� ��
������F��ֱ�߽�y���������ڵ�G��ʹ��GFO=30������ֱ���ϵĵ�P��m��n������O�Ĺ����㣬��m��ȡֵ��Χ��
��2�����߶�EF�ϵ����е㶼��ij��Բ�Ĺ����㣬�����Բ�İ뾶r��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
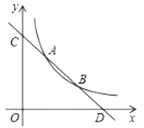
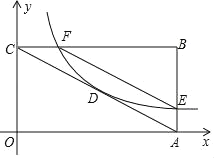
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�����߷ֱ���x�ᡢy���ϣ�D�ǶԽ��ߵĽ��㣬������������y��![]() ��ͼ����D���������OABC������AB��BC�ֱ��ڵ�E��F��
��ͼ����D���������OABC������AB��BC�ֱ��ڵ�E��F��
��1����D��������4��2��
����OA�ij����� ����AB�ij����� ����
�����ж�EF�Ƿ���ACƽ�У���˵�����ɣ�
����x�����Ƿ����һ��P��ʹPD+PE��ֵ��С�������ڣ��������P�����꼰��ʱPD+PE�ij����������ڣ���˵�����ɣ�
��2������D������Ϊ��m��n������m��0��n��0����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�з���һ������ֽƬABCO����ֽƬ���ۺ�Bǡ������![]() ���ϣ���Ϊ
���ϣ���Ϊ![]() ���ۺ�ΪCE��ֱ��CE�Ĺ�ϵʽ��
���ۺ�ΪCE��ֱ��CE�Ĺ�ϵʽ��![]() ����
����![]() ���ཻ�ڵ�F����AE��3��
���ཻ�ڵ�F����AE��3��
��1����OC���ȣ�
��2�����![]() �����ꣻ
�����ꣻ
��3�������ABCO�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com