
【题目】如图,在△ABC中,∠ABC=90°,BD为AC边的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AB=12,BC=5,则四边形BDFG的周长为 . 
【答案】26
【解析】解:∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,
∴BD=DF= ![]() AC,
AC,
∴四边形BGFD是菱形,
∴BG=GF=DF=BD,
∵在△ABC中,∠ABC=90°,AB=12,BC=5,由勾股定理得:AC=13,
∵BD为△ACB的中线,
∴BD= ![]() AC=
AC= ![]() ,
,
∴BG=GF=DF=BD= ![]() ,
,
故四边形BDFG的周长=4GF=26.
所以答案是:26.
【考点精析】本题主要考查了直角三角形斜边上的中线和勾股定理的概念的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图1,点A,B分别是二次函数y=2x2的图象上的两个点,A、B的横坐标分别为a,b(a<0,b>0),点P(0,t)是抛物线对称轴上的任意一点.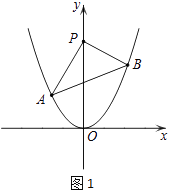
(1)当a+b=0时,探究是否存在t,使得△PAB是以AB为底的等腰三角形?若存在,请直接写出t、a、b的其中一组值;若不存在,请说明理由;
(2)当a+b≠0时,探究是否存在t,使得△PAB是以AB为底的等腰三角形?若存在,请写出t的取值范围,并用含t的代数式表示a2+b2的值;若不存在,请说明理由;
(3)如图2作边长为4的正方形ACDE(A、C、D、E按逆时针排列),使得AC∥x轴,若边CD与二次函数的图象总有交点,求a的取值范围.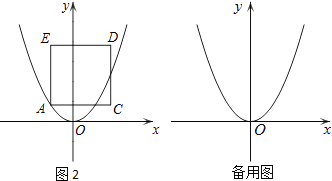
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,P为AD上一点,连接BP,CP,过C作CE⊥BP于点E,连接ED交PC于点F.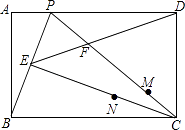
(1)求证:△ABP∽△ECB;
(2)若点E恰好为BP的中点,且AB=3,AP=k(0<k<3).
①求 ![]() 的值(用含k的代数式表示);
的值(用含k的代数式表示);
②若M、N分别为PC,EC上的任意两点,连接NF,NM,当k= ![]() 时,求NF+NM的最小值.
时,求NF+NM的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠ACB=90°,现按如下步骤作图:
①分别以A,C为圆心,a为半径(a> ![]() AC)作弧,两弧分别交于M,N两点;
AC)作弧,两弧分别交于M,N两点;
②过M,N两点作直线MN交AB于点D,交AC于点E;
③将△ADE绕点E顺时针旋转180°,设点D的像为点F.
(1)请在图中直线标出点F并连接CF;
(2)求证:四边形BCFD是平行四边形;
(3)当∠B为多少度时,四边形BCFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售A,B两种产品,根据市场调研,确定两条信息:
信息1:销售A种产品所获利润y:(万元)与销售产品x(吨)之间存在二次函数关系,如图所示:
信息2:销售B种产品所获利润y(万元)与销售产品x(吨)之间存在正比例函数关系y2=0.3x.
根据以上信息,解答下列问题;
(1)求二次函数解析式;
(2)该公司准备购进A、B两种产品共10吨,求销售A、B两种产品获得的利润之和最大是多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(3,2)和点M(m,n)都在反比例函数y= ![]() (x>0)的图象上.
(x>0)的图象上.
(1)求k的值,并求当m=4时,直线AM的解析式;
(2)过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴于点Q,试说明四边形ABPQ是平行四边形;
(3)在(2)的条件下,四边形ABPQ能否为菱形?若能,请求出m的值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2015次相遇在边上. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC. 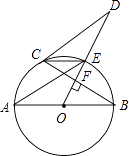
(1)求证:直线CD为⊙O的切线;
(2)若AB=5,BC=4,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两公司为“见义勇为基金会”各捐款60000元,已知乙公司比甲公司人均多捐40元,甲公司的人数比乙公司的人数多20%.
请你根据以上信息,提出一个用分式方程解决的问题,并写出解答过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com